
���}��1������2������3�������x���}��ÿС�}7�֣�Ո�������x2�}���𣬝M��14�֣�����������t��������ǰ���}Ӌ(j��)�֡�����r(sh��)������2B�U�P�ڴ��}���ϰ����x�}Ŀ����(y��ng)���}̖Ϳ�ڣ��������x�}̖������̖��.
��1������С�}�M��7�֣��x��4-4������(bi��o)ϵ�c����(sh��)����
��ֱ������(bi��o)ϵ��ԭ�c(di��n) ��O�c(di��n)��
��O�c(di��n)�� �S�������S��O�S����֪�c(di��n)
�S�������S��O�S����֪�c(di��n) ��ֱ������(bi��o)�飨1��-5�����c(di��n)
��ֱ������(bi��o)�飨1��-5�����c(di��n) �ĘO����(bi��o)��
�ĘO����(bi��o)�� ��ֱ��
��ֱ�� �^�c(di��n)
�^�c(di��n) ���҃Aб�Ǟ�
���҃Aб�Ǟ� ���A
���A ��
�� ��A�ġ�
��A�ġ� ��돽��
��돽��
��I����ֱ�� �ą���(sh��)���̺͈A
�ą���(sh��)���̺͈A �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�
��II��ԇ�ж�ֱ�� �͈A
�͈A ��λ���P(gu��n)ϵ.
��λ���P(gu��n)ϵ.
��2������С�}�M��7�֣��x��4-4������c׃�Q
������ ���M(j��n)�ЙM����(bi��o)�s��ԭ����һ�룬�v����(bi��o)���ֲ�׃����s׃�Q�������P(gu��n)��
���M(j��n)�ЙM����(bi��o)�s��ԭ����һ�룬�v����(bi��o)���ֲ�׃����s׃�Q�������P(gu��n)�� �S�ķ���׃�Q׃?y��u)�����
�S�ķ���׃�Q׃?y��u)����� ��������
�������� �ķ��̣�
�ķ��̣�
��3������С�}�M��7�֣��x��4-5������ʽ�x�v
�P(gu��n)�� ��һԪ���η���
��һԪ���η��� ������
������ �o��(sh��)������(sh��)��(sh��)
�o��(sh��)������(sh��)��(sh��) ��ȡֵ����.
��ȡֵ����.
��1����I��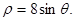 ��II��ֱ��
��II��ֱ��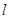 �c�AC���x
�c�AC���x
��2��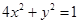
��3��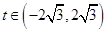
����������1���⣨I��ֱ��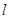 �ą���(sh��)���̞�
�ą���(sh��)���̞�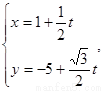 ��t�酢��(sh��)��
��t�酢��(sh��)��
�AC�ĘO����(bi��o)���̞�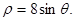
��II����?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052107184521877182/SYS201205210720596875256770_DA.files/image006.png">����(y��ng)��ֱ������(bi��o)�飨0��4��ֱ��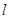 ������ͨ���̞�
������ͨ���̞�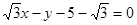 ,�A�ĵ�
,�A�ĵ�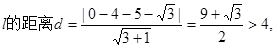 ����ֱ��
����ֱ��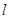 �c�AC���x��
�c�AC���x��
��2���⣺
����s׃�QM=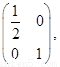 ����׃�QN=
����׃�QN=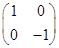 ,�� A=NM=
,�� A=NM=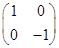
 =
=
��A׃�Q�µõ�����C��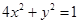 ��
��
��3��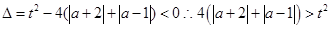 ��
�� ���������
���������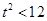
�Ķ�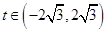 .
.


 ���I(y��)�o��(d��o)ϵ�д�
���I(y��)�o��(d��o)ϵ�д� ͬ���W(xu��)��һ�n�ྚϵ�д�
ͬ���W(xu��)��һ�n�ྚϵ�д� ��(j��ng)���ܾ�ϵ�д�
��(j��ng)���ܾ�ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
|
| �� |
|
| �� |
|
| �� |
| 4 |
| ||
| 2 |
|
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
|
| �� |
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2011�ø���ʡ�ĵ���У(li��n)�������όW(xu��)�ڵڶ����¿����Ɣ�(sh��)�W(xu��)�� �}�ͣ�����}
����С�}�M��14�֣����}��1������2������3�������x���}��ÿС�}7�֣����x2�}���𣬝M��14�֣�����������t��������ǰ���}Ӌ(j��)�֡�����r(sh��)������2B�U�P�ڴ��}���ϰ����x�}Ŀ����(y��ng)���}̖Ϳ�ڣ��������x�}̖������̖�С�
��1��(��С�}�M��7��) �x��4-2:����c׃�Q
��֪ ����
���� ������(y��ng)��׃�Q
������(y��ng)��׃�Q ��ֱ��
��ֱ�� ׃�Q����������(sh��)��(sh��)
׃�Q����������(sh��)��(sh��) ������
������ �����ꇡ�
�����ꇡ�
��2�������}�M��7�֣��x��4-4������(bi��o)ϵ�c����(sh��)����
��ֱ֪�� �ą���(sh��)���̣�
�ą���(sh��)���̣� ��
�� �酢��(sh��)���͈A
�酢��(sh��)���͈A �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣� ��
��
�ٌ�ֱ�� �ą���(sh��)���̻�����ͨ���̣��A
�ą���(sh��)���̻�����ͨ���̣��A �ĘO����(bi��o)���̻���ֱ������(bi��o)���̣�
�ĘO����(bi��o)���̻���ֱ������(bi��o)���̣�
���Д�ֱ�� �͈A
�͈A ��λ���P(gu��n)ϵ��
��λ���P(gu��n)ϵ��
��3�������}�M��7�֣��x��4-5������ʽ�x�v
��֪����(sh��)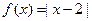
�ٽⲻ��ʽ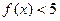 ��
��
���C���������� ������ʽ
������ʽ ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2010-2011�W(xu��)�긣��ʡ�ĵ���У(li��n)�������όW(xu��)�ڵڶ����¿����Ɣ�(sh��)�W(xu��)�� �}�ͣ�����}
����С�}�M��14�֣����}��1������2������3�������x���}��ÿС�}7�֣����x2�}���𣬝M��14�֣�����������t��������ǰ���}Ӌ(j��)�֡�����r(sh��)������2B�U�P�ڴ��}���ϰ����x�}Ŀ����(y��ng)���}̖Ϳ�ڣ��������x�}̖������̖�С�
��1��(��С�}�M��7��) �x��4-2:����c׃�Q
��֪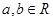 ����
���� ������(y��ng)��׃�Q
������(y��ng)��׃�Q ��ֱ��
��ֱ�� ׃�Q����������(sh��)��(sh��)
׃�Q����������(sh��)��(sh��) ������
������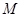 �����ꇡ�
�����ꇡ�
��2�������}�M��7�֣��x��4-4������(bi��o)ϵ�c����(sh��)����
��ֱ֪�� �ą���(sh��)���̣�
�ą���(sh��)���̣� ��
�� �酢��(sh��)���͈A
�酢��(sh��)���͈A �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣� ��
��
�ٌ�ֱ�� �ą���(sh��)���̻�����ͨ���̣��A
�ą���(sh��)���̻�����ͨ���̣��A �ĘO����(bi��o)���̻���ֱ������(bi��o)���̣�
�ĘO����(bi��o)���̻���ֱ������(bi��o)���̣�
���Д�ֱ�� �͈A
�͈A ��λ���P(gu��n)ϵ��
��λ���P(gu��n)ϵ��
��3�������}�M��7�֣��x��4-5������ʽ�x�v
��֪����(sh��)
�ٽⲻ��ʽ ��
��
���C���������� ������ʽ
������ʽ ����.
����.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com