
【題目】離心率為![]() 的橢圓
的橢圓![]() 經過點
經過點![]() ,
,![]() 是坐標原點.
是坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)是否存在圓心在原點的圓,使得該圓的任意一條切線與橢圓![]() 恒有兩個交點
恒有兩個交點![]() ,且
,且![]() ?若存在,求出該圓的方程,并求
?若存在,求出該圓的方程,并求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
【答案】(1)![]() ;
;
(2)存在,理由見解析;圓的方程為![]() ;
;![]() .
.
【解析】
(1)利用離心率和橢圓所過點聯立方程組可求橢圓的方程;
(2)先假設存在符合要求的圓,利用![]() 求出圓的切線,結合弦長公式表示出
求出圓的切線,結合弦長公式表示出![]() ,利用基本不等式求解范圍.
,利用基本不等式求解范圍.
(1)因為橢圓![]() 經過點
經過點![]() ,所以
,所以![]() ;
;
又離心率為![]() ,所以
,所以![]() ,結合
,結合![]() 可得
可得![]() ,
,
所以橢圓![]() 的方程為
的方程為![]() .
.
(2)假設存在圓心在原點的圓,使得該圓的任意一條切線與橢圓![]() 恒有兩個交點
恒有兩個交點![]() ,且
,且![]() ,設圓的切線方程為
,設圓的切線方程為![]() ,
,![]() .
.
聯立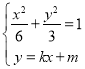 得
得![]() ,
,
![]()
即![]() .
.
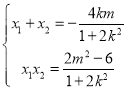
![]()
因為![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ;
;
因為圓的切線方程為![]() ,所以圓的半徑為
,所以圓的半徑為![]() ,
,![]() ,所求圓的方程為
,所求圓的方程為![]() .
.
由![]() 及
及![]() 可得
可得![]() ,即
,即![]() 或
或![]() ;
;
當圓的切線斜率不存在時,切線方程為![]() ,切線與橢圓的交點為
,切線與橢圓的交點為![]() 或者
或者![]() ,均滿足
,均滿足![]() .
.
綜上可知,存在圓心在原點的圓,使得該圓的任意一條切線與橢圓![]() 恒有兩個交點
恒有兩個交點![]() ,且
,且![]() .
.
因為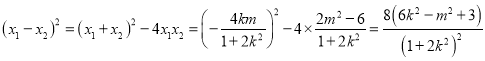
所以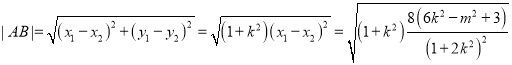
![]()
當![]() 時,由于
時,由于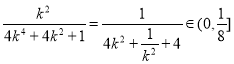 ,所以
,所以![]() ,當且僅當
,當且僅當![]() 時,取到最大值3;
時,取到最大值3;
當![]() 時,
時,![]() ;
;
當斜率不存在時,直線![]() 與橢圓交于
與橢圓交于![]() 或者
或者![]() 此時
此時![]() .
.
綜上可知,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】近年來,隨著我國汽車消費水平的提高,二手車流通行業得到迅猛發展.某汽車交易市場對2017年成交的二手車交易前的使用時間(以下簡稱“使用時間”)進行統計,得到頻率分布直方圖如圖1.


圖1 圖2
(1)記“在![]() 年成交的二手車中隨機選取一輛,該車的使用年限在
年成交的二手車中隨機選取一輛,該車的使用年限在![]() ”為事件
”為事件![]() ,試估計
,試估計![]() 的概率;
的概率;
(2)根據該汽車交易市場的歷史資料,得到散點圖如圖2,其中![]() (單位:年)表示二手車的使用時間,
(單位:年)表示二手車的使用時間,![]() (單位:萬元)表示相應的二手車的平均交易價格.由散點圖看出,可采用
(單位:萬元)表示相應的二手車的平均交易價格.由散點圖看出,可采用![]() 作為二手車平均交易價格
作為二手車平均交易價格![]() 關于其使用年限
關于其使用年限![]() 的回歸方程,相關數據如下表(表中
的回歸方程,相關數據如下表(表中![]() ,
,![]() ):
):

①根據回歸方程類型及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②該汽車交易市場對使用8年以內(含8年)的二手車收取成交價格![]() 的傭金,對使用時間8年以上(不含8年)的二手車收取成交價格
的傭金,對使用時間8年以上(不含8年)的二手車收取成交價格![]() 的傭金.在圖1對使用時間的分組中,以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據,計算該汽車交易市場對成交的每輛車收取的平均傭金.
的傭金.在圖1對使用時間的分組中,以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據,計算該汽車交易市場對成交的每輛車收取的平均傭金.
附注:①對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ;
;
②參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我區的中小學辦學條件在政府的教育督導下,迅速得到改變.督導一年后.分別隨機抽查了高中(用![]() 表示)與初中(用
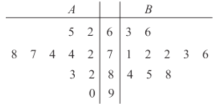
表示)與初中(用![]() 表示)各10所學校.得到相關指標的綜合評價得分(百分制)的莖葉圖如圖所示.則從莖葉圖可得出正確的信息為(80分及以上為優秀)( )
表示)各10所學校.得到相關指標的綜合評價得分(百分制)的莖葉圖如圖所示.則從莖葉圖可得出正確的信息為(80分及以上為優秀)( )
①高中得分與初中得分的優秀率相同
②高中得分與初中得分的中位數相同
③高中得分的方差比初中得分的方差大
④高中得分與初中得分的平均分相同
A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
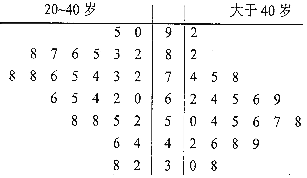
【題目】某公司即將推車一款新型智能手機,為了更好地對產品進行宣傳,需預估市民購買該款手機是否與年齡有關,現隨機抽取了50名市民進行購買意愿的問卷調查,若得分低于60分,說明購買意愿弱;若得分不低于60分,說明購買意愿強,調查結果用莖葉圖表示如圖所示.
(1)根據莖葉圖中的數據完成![]() 列聯表,并判斷是否有95%的把握認為市民是否購買該款手機與年齡有關?
列聯表,并判斷是否有95%的把握認為市民是否購買該款手機與年齡有關?
購買意愿強 | 購買意愿弱 | 合計 | |
20-40歲 | |||
大于40歲 | |||
合計 |
(2)從購買意愿弱的市民中按年齡進行分層抽樣,共抽取5人,從這5人中隨機抽取2人進行采訪,記抽到的2人中年齡大于40歲的市民人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附: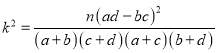 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一款擊鼓小游戲的規則如下:每盤游戲都需擊鼓三次,每次擊鼓后要么出現一次音樂,要么不出現音樂;每盤游戲擊鼓三次后,出現三次音樂獲得150分,出現兩次音樂獲得100分,出現一次音樂獲得50分,沒有出現音樂則獲得-300分.設每次擊鼓出現音樂的概率為![]() ,且各次擊鼓出現音樂相互獨立.
,且各次擊鼓出現音樂相互獨立.
(1)若一盤游戲中僅出現一次音樂的概率為![]() ,求
,求![]() 的最大值點
的最大值點![]() ;
;
(2)以(1)中確定的![]() 作為
作為![]() 的值,玩3盤游戲,出現音樂的盤數為隨機變量
的值,玩3盤游戲,出現音樂的盤數為隨機變量![]() ,求每盤游戲出現音樂的概率
,求每盤游戲出現音樂的概率![]() ,及隨機變量
,及隨機變量![]() 的期望
的期望![]() ;
;
(3)玩過這款游戲的許多人都發現,若干盤游戲后,與最初的分數相比,分數沒有增加反而減少了.請運用概率統計的相關知識分析分數減少的原因.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x﹣a|+|x![]() |(a>0).
|(a>0).
(1)若不等式f(x)﹣| x![]() |≥4x的解集為{x|x≤1},求實數a的值;
|≥4x的解集為{x|x≤1},求實數a的值;
(2)證明:f(x)![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com