【題目】如圖，在四棱錐
中，底面ABCD為直角梯形，
，
平面ABCD，E是棱PC上的一點.
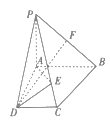
（1）證明：平面
平面
.
（2）若
，F是PB的中點，
，
，求直線DF與平面
所成角的正弦值.
發散思維新課堂系列答案科目：高中數學 來源： 題型：
【題目】如圖,五邊形
中,四邊形
為長方形,
為邊長為
的正三角形,將沿
折起,使得點
在平面上的射影恰好在
上.
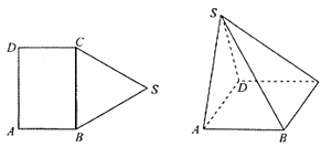
（Ⅰ）當
時,證明:平面
平面
；
（Ⅱ）若
,求平面與平面
所成二面角的余弦值的絕對值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】撫州市某中學利用周末組織教職員工進行了一次秋季登軍峰山健身的活動，有
人參加，現將所有參加人員按年齡情況分為
，
，
，
，
，
，
等七組，其頻率分布直方圖如下圖所示．已知之間的參加者有4人．
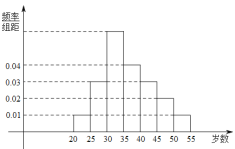
（1）求和之間的參加者人數
；
（2）組織者從
之間的參加者（其中共有
名女教師包括甲女，其余全為男教師）中隨機選取
名擔任后勤保障工作，求在甲女必須入選的條件下，選出的女教師的人數為2人的概率.
（3）已知和之間各有
名數學教師，現從這兩個組中各選取人擔任接待工作，設兩組的選擇互不影響，求兩組選出的人中都至少有
名數學教師的概率?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在正方體AC1中，E，F分別為D1C1，B1C1的中點，AC∩BD＝P，A1C1∩EF＝Q，如圖.
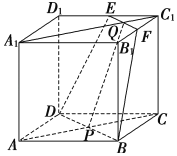
（1）若A1C交平面EFBD于點R，證明:P，Q，R三點共線.
（2）線段AC上是否存在點M，使得平面B1D1M∥平面EFBD，若存在確定M的位置，若不存在說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
兩點分別在
軸和
軸上運動，且
，若動點
滿足
.
（1）求出動點P的軌跡對應曲線C的標準方程；
（2）一條縱截距為2的直線
與曲線C交于P，Q兩點，若以PQ直徑的圓恰過原點，求出直線方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
， (
為參數， 
為傾斜角).以坐標原點為極點， 
軸的正半軸為極軸建立極坐標系，曲線
的直角坐標方程為
.
（Ⅰ）將曲線
的直角坐標方程化為極坐標方程；
（Ⅱ）設點
的直角坐標為
，直線
與曲線
的交點為
、
，求
的取值范圍.
【答案】（I）
；（II）
.
【解析】試題分析：（Ⅰ）將由
代入
，化簡即可得到曲線
的極坐標方程；（Ⅱ）將
的參數方程
代入
，得
，根據直線參數方程的幾何意義，利用韋達定理結合輔助角公式，由三角函數的有界性可得結果.
試題解析：（Ⅰ）由
及
，得
，即
所以曲線
的極坐標方程為
（II）將
的參數方程
代入
，得
∴
, 所以
，又
，
所以
，且
,
所以
,
由
，得
，所以
.
故
的取值范圍是
.
【題型】解答題
【結束】
23
【題目】已知
、
、
均為正實數.
（Ⅰ）若
，求證： 
（Ⅱ）若
，求證： 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
