
【題目】已知四棱錐P-ABCD的體積為![]() ,其三視圖如圖所示,其中正視圖為等腰三角形,側視圖為直角三角形,俯視圖是直角梯形.
,其三視圖如圖所示,其中正視圖為等腰三角形,側視圖為直角三角形,俯視圖是直角梯形.

(1)求正視圖的面積;
(2)求四棱錐P-ABCD的側面積.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)根據四棱錐的體積得PA=![]() ,進而得正視圖的面積;
,進而得正視圖的面積;
(2)過A作AE∥CD交BC于E,連接PE,確定四個側面積面積S△PAB,S△PAD, S△PCD, S△PBC求和即可.
試題解析:
(1) 如圖所示四棱錐P-ABCD的高為PA,底面積為S=![]() ·CD=
·CD=![]() ×1=
×1=![]()
∴四棱錐P-ABCD的體積V四棱錐P-ABCD=![]() S·PA=
S·PA=![]() ×
×![]() ·PA=
·PA=![]() ,∴PA=
,∴PA=![]()
∴正視圖的面積為S=![]() ×2×
×2×![]() =
=![]() .
.
(2)如圖所示,過A作AE∥CD交BC于E,連接PE.根據三視圖可知,E是BC的中點,
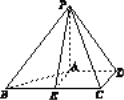
且BE=CE=1,AE=CD=1,且BC⊥AE,AB=![]()
又PA⊥平面ABCD,∴PA⊥BC,PA⊥DC,PD=![]() ,∴BC⊥面PAE,∴BC⊥PE,
,∴BC⊥面PAE,∴BC⊥PE,
又DC⊥AD,∴DC⊥面PAD,∴DC⊥PD,且PA⊥平面ABCD.∴PA⊥AE,
∴PE2=PA2+AE2=3.∴PE=![]() .
.
∴四棱錐P-ABCD的側面積為
S=S△PAB+ S△PAD+ S△PCD+ S△PBC=![]() ·
·![]() ·
·![]() +
+![]() ·
·![]() ·1+
·1+![]() ·1·
·1·![]() +
+![]() ·2·
·2·![]() =
=![]() .
.


科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象過點
的圖象過點![]() ,且與
,且與![]() 軸有唯一的交點
軸有唯一的交點![]() .
.
(1)求![]() 的表達式;
的表達式;
(2)設函數![]() ,若
,若![]() 上是單調函數,求實數
上是單調函數,求實數![]() 的取值范圍;
的取值范圍;
(3)設函數![]() ,記此函數的最小值為
,記此函數的最小值為![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga ![]() (a>0且a≠1)是奇函數.
(a>0且a≠1)是奇函數.
(1)求實數m的值;
(2)判斷函數f(x)在區間(1,+∞)上的單調性并說明理由;
(3)當x∈(n,a﹣2)時,函數f(x)的值域為(1,+∞),求實數n,a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】綜合題。
(1)已知f( ![]() +1)=x+2
+1)=x+2 ![]() ,求f(x)的解析式;
,求f(x)的解析式;
(2)已知f(x)是一次函數,且滿足3f(x+1)﹣2f(x﹣1)=2x+17,求f(x)的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
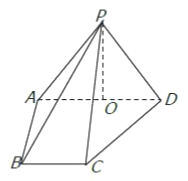
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,側棱
,側棱![]() ,底面
,底面![]() 為直角梯形,其中
為直角梯形,其中![]() 為
為![]() 中點.
中點.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)線段![]() 上是否存在
上是否存在![]() ,使得它到平面
,使得它到平面![]() 的距離為
的距離為![]() ?若存在,求出
?若存在,求出![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市在發展過程中,交通狀況逐漸受到有關部門的關注,據有關統計數據顯示,從上午6點到中午12點,車輛通過該市某一路段的用時y(分鐘)與車輛進入該路段的時刻t之間的關系可近似地用如下函數給出: y= 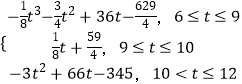
求從上午6點到中午12點,通過該路段用時最多的時刻.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四面體P﹣ABCD中,△ABD是邊長為2的正三角形,PC⊥底面ABCD,AB⊥BP,BC= ![]() .
. 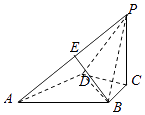
(1)求證:PA⊥BD;
(2)已知E是PA上一點,且BE∥平面PCD.若PC=2,求點E到平面ABCD的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com