
【題目】函數![]() ,下列對函數
,下列對函數![]() 的性質描述正確的是( )
的性質描述正確的是( )
A.函數![]() 的圖象關于點
的圖象關于點![]() 對稱
對稱
B.若![]() ,則函數f(x)有極值點
,則函數f(x)有極值點
C.若![]() ,函數
,函數![]() 在區間
在區間![]() 單調遞減
單調遞減
D.若函數![]() 有且只有3個零點,則a的取值范圍是
有且只有3個零點,則a的取值范圍是![]()
【答案】A
【解析】
利用函數的對稱性即可判斷選項A是否正確;對函數![]() 求導,分別就
求導,分別就![]() 和
和![]() 進行討論,即可判斷選項B、C是否正確;函數
進行討論,即可判斷選項B、C是否正確;函數![]() 有三個不同的零點,根據函數的單調性,可知函數
有三個不同的零點,根據函數的單調性,可知函數![]() 的極小值小于0,極大值大于0,列出不等式組,求出a的取值范圍,由此即可判斷選項D是否正確.
的極小值小于0,極大值大于0,列出不等式組,求出a的取值范圍,由此即可判斷選項D是否正確.
對于選項A,因為![]() ,所以
,所以![]() ,所以
,所以![]() ,所以函數
,所以函數![]() 的圖象關于點
的圖象關于點![]() 對稱,故選項A正確;
對稱,故選項A正確;
對于選項B,由![]() ,當
,當![]() 時,
時,![]() ,函數
,函數![]() 在定義域內為增函數,此時函數
在定義域內為增函數,此時函數![]() 沒有極值點,故選項B錯誤;
沒有極值點,故選項B錯誤;
對于選項C,當![]() 時,由
時,由![]() ,解得
,解得![]() .
.
又∵![]() 時,
時,![]() ,所以函數
,所以函數![]() 在區間
在區間![]() 單調遞增,故選項C錯誤;
單調遞增,故選項C錯誤;
對于選項D,由![]() ,
,
當![]() 時,
時,![]() ,函數
,函數![]() 在定義域內為增函數,故不存在三個零點,不符合題意;
在定義域內為增函數,故不存在三個零點,不符合題意;
當![]() 時,由
時,由![]() ,解得
,解得![]() .
.
又∵![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
∴函數![]() 單調遞增區間為
單調遞增區間為![]() 和
和![]() ,單調遞減區間為
,單調遞減區間為![]() ,
,
∴函數的極小值![]() 和極大值
和極大值![]() .
.
∵函數![]() 有三個不同的零點,
有三個不同的零點,
∴ 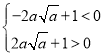 , 解得
, 解得![]() ,故選項D錯誤.
,故選項D錯誤.
故選:A.


科目:高中數學 來源: 題型:
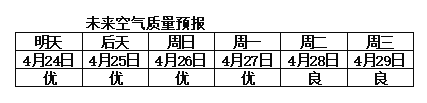
【題目】假設今天是4月23日,某市未來六天的空氣質量預報情況如下圖所示.該市有甲、乙、丙三人計劃在未來六天(4月24日~4月29日)內選擇一天出游,甲只選擇空氣質量為優的一天出游,乙不選擇周一出游,丙不選擇明天出游,且甲與乙不選擇同一天出游,則這三人出游的不同方法數為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司準備上市一款新型轎車零配件,上市之前擬在其一個下屬4S店進行連續30天的試銷.定價為1000元/件.試銷結束后統計得到該4S店這30天內的日銷售量(單位:件)的數據如下表:
日銷售量 | 40 | 60 | 80 | 100 |
頻數 | 9 | 12 | 6 | 3 |
(1)若該4S店試銷期間每個零件的進價為650元/件,求試銷連續30天中該零件日銷售總利潤不低于24500元的頻率;
(2)試銷結束后,這款零件正式上市,每個定價仍為1000元,但生產公司對該款零件不零售,只提供零件的整箱批發,大箱每箱有60件,批發價為550元/件;小箱每箱有45件,批發價為600元/件.該4S店決定每天批發兩箱,根據公司規定,當天沒銷售出的零件按批發價的9折轉給該公司的另一下屬4S店.假設該4店試銷后的連續30天的日銷售量(單位:件)的數據如下表:
日銷售量 | 50 | 70 | 90 | 110 |
頻數 | 5 | 15 | 8 | 2 |
(ⅰ)設該4S店試銷結束后連續30天每天批發兩大箱,這30天這款零件的總利潤;
(ⅱ)以總利潤作為決策依據,該4S店試銷結束后連續30天每天應該批發兩大箱還是兩小箱?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年寒假是特殊的寒假,因為抗擊疫情全體學生只能在家進行網上在線學習,為了研究學生在網上學習的情況,某學校在網上隨機抽取120名學生對線上教育進行調查,其中男生與女生的人數之比為11∶13,其中男生30人對于線上教育滿意,女生中有15名表示對線上教育不滿意.
(1)完成![]() 列聯表,并回答能否有99%的把握認為對“線上教育是否滿意與性別有關”;
列聯表,并回答能否有99%的把握認為對“線上教育是否滿意與性別有關”;
滿意 | 不滿意 | 總計 | |
男生 | 30 | ||
女生 | 15 | ||
合計 | 120 |
(2)從被調查的對線上教育滿意的學生中,利用分層抽樣抽取8名學生,再在8名學生中抽取3名學生,作線上學習的經驗介紹,其中抽取男生的個數為![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
參考公式:附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等腰直角△![]() 內接于拋物線
內接于拋物線![]() (
(![]() ),其中
),其中![]() 為拋物線的頂點,
為拋物線的頂點,![]() ,△
,△![]() 的面積是16.
的面積是16.
(1)求拋物線![]() 的方程;
的方程;
(2)拋物線![]() 的焦點為
的焦點為![]() ,過
,過![]() 的直線交拋物線于
的直線交拋物線于![]()
![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,若
,若![]() ,
,![]() ,證明:
,證明:![]() 是一個定值.
是一個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著食品安全問題逐漸引起人們的重視,有機、健康的高端綠色蔬菜越來越受到消費者的歡迎,同時生產—運輸—銷售一體化的直銷供應模式,不僅減少了成本,而且減去了蔬菜的二次污染等問題.
(1)在有機蔬菜的種植過程中,有機肥料使用是必不可少的.根據統計某種有機蔬菜的產量與有機肥料的用量有關系,每個有機蔬菜大棚產量的增加量![]() (百斤)與使用堆漚肥料
(百斤)與使用堆漚肥料![]() (千克)之間對應數據如下表
(千克)之間對應數據如下表
使用堆漚肥料 | 2 | 4 | 5 | 6 | 8 |
產量的增加量 | 3 | 4 | 4 | 4 | 5 |
依據表中的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;并根據所求線性回歸方程,估計如果每個有機蔬菜大棚使用堆漚肥料10千克,則每個有機蔬菜大棚產量增加量
;并根據所求線性回歸方程,估計如果每個有機蔬菜大棚使用堆漚肥料10千克,則每個有機蔬菜大棚產量增加量![]() 是多少百斤?
是多少百斤?
(2)某大棚蔬菜種植基地將采摘的有機蔬菜以每份三斤稱重并保鮮分裝,以每份10元的價格銷售到生鮮超市.“樂購”生鮮超市以每份15元的價格賣給顧客,如果當天前8小時賣不完,則超市通過促銷以每份5元的價格賣給顧客(根據經驗,當天能夠把剩余的有機蔬菜都低價處理完畢,且處理完畢后,當天不再進貨).該生鮮超市統計了100天有機蔬菜在每天的前8小時內的銷售量(單位:份),制成如下表格(注:![]() ,且
,且![]() );
);
前8小時內的銷售量(單位:份) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
頻數 | 10 | x | 16 | 6 | 15 | 13 | y |
若以100天記錄的頻率作為每日前8小時銷售量發生的概率,該生鮮超市當天銷售有機蔬菜利潤的期望值為決策依據,當購進17份比購進18份的利潤的期望值大時,求![]() 的取值范圍.
的取值范圍.
附:回歸直線方程為![]() ,其中
,其中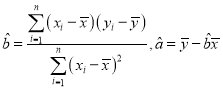 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫院為篩查某種疾病,需要檢驗血液是否為陽性,現有![]() (
(![]() )份血液樣本,有以下兩種檢驗方式:(1)逐份檢驗,則需要檢驗
)份血液樣本,有以下兩種檢驗方式:(1)逐份檢驗,則需要檢驗![]() 次;(2)混合檢驗,將其中
次;(2)混合檢驗,將其中![]() (
(![]() 且
且![]() )份血液樣本分別取樣混合在一起檢驗.若檢驗結果為陰性,這
)份血液樣本分別取樣混合在一起檢驗.若檢驗結果為陰性,這![]() 份的血液全為陰性,因而這
份的血液全為陰性,因而這![]() 份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這
份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這![]() 份血液究竟哪幾份為陽性,就要對這
份血液究竟哪幾份為陽性,就要對這![]() 份再逐份檢驗,此時這
份再逐份檢驗,此時這![]() 份血液的檢驗次數總共為
份血液的檢驗次數總共為![]() 次.假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為
次.假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為![]() .
.
(1)假設有5份血液樣本,其中只有2份樣本為陽性,若采用逐份檢驗方式,求恰好經過4次檢驗就能把陽性樣本全部檢驗出來的概率.
(2)現取其中![]() (
(![]() 且
且![]() )份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為
)份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為![]() ,采用混合檢驗方式,樣本需要檢驗的總次數為
,采用混合檢驗方式,樣本需要檢驗的總次數為![]()
(ⅰ)試運用概率統計的知識,若![]()
![]() ,試求
,試求![]() 關于
關于![]() 的函數關系式
的函數關系式![]() ;
;
(ⅱ)若![]() ,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數期望值更少,求
,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數期望值更少,求![]() 的最大值.
的最大值.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】針對時下的“抖音熱”,某校團委對“學生性別和喜歡抖音是否有關”作了一次調查,其中被調查的男女生人數相同,男生喜歡抖音的人數占男生人數的![]() ,女生喜歡抖音的人數占女生人數
,女生喜歡抖音的人數占女生人數![]() ,若有95%的把握認為是否喜歡抖音和性別有關則調查人數中男生可能有( )人
,若有95%的把握認為是否喜歡抖音和性別有關則調查人數中男生可能有( )人
附表:
| 0.050 | 0.010 |
k | 3.841 | 6.635 |
附:
A.25或45B.45C.45或60D.75或60
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的左焦點為
)的左焦點為![]() ,點
,點![]() 為橢圓
為橢圓![]() 上任意一點,且
上任意一點,且![]() 的最小值為
的最小值為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設O為坐標原點,若動直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 、
、![]() (
(![]() 、
、![]() 都在
都在![]() 軸上方),且
軸上方),且![]() .
.
(i)當![]() 為橢圓與
為橢圓與![]() 軸正半軸的交點時,求直線
軸正半軸的交點時,求直線![]() 的方程;
的方程;
(ii)對于動直線![]() ,是否存在一個定點,無論
,是否存在一個定點,無論![]() 如何變化,直線
如何變化,直線![]() 總經過此定點?若存在,求出該定點的坐標;若不存在,請說明理由.
總經過此定點?若存在,求出該定點的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com