
【題目】已知某校6個學生的數學和物理成績如下表:
學生的編號 | 1 | 2 | 3 | 4 | 5 | 6 |
數學 | 89 | 87 | 79 | 81 | 78 | 90 |
物理 | 79 | 75 | 77 | 73 | 72 | 74 |
(1)若在本次考試中,規定數學在80分以上(包括80分)且物理在75分以上(包括75分)的學生為理科小能手.從這6個學生中抽出2個學生,設![]() 表示理科小能手的人數,求
表示理科小能手的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)通過大量事實證明發現,一個學生的數學成績和物理成績具有很強的線性相關關系,在上述表格是正確的前提下,用![]() 表示數學成績,用
表示數學成績,用![]() 表示物理成績,求
表示物理成績,求![]() 與
與![]() 的回歸方程.
的回歸方程.
參考數據和公式:![]() ,其中
,其中 ,
,![]() .
.
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為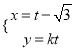 (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為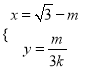 (
(![]() 為參數),設
為參數),設![]() 與
與![]() 的交點為
的交點為![]() ,當
,當![]() 變化時,
變化時, ![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)寫出![]() 的普遍方程及參數方程;
的普遍方程及參數方程;
(2)以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系,設曲線
軸正半軸為極軸建立極坐標系,設曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() 為曲線
為曲線![]() 上的動點,求點
上的動點,求點![]() 到
到![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() x2+alnx.
x2+alnx.
(1)若a=﹣1,求函數f(x)的極值,并指出極大值還是極小值;
(2)若a=1,求函數f(x)在[1,e]上的最值;
(3)若a=1,求證:在區間[1,+∞)上,函數f(x)的圖象在g(x)=![]() x3的圖象下方.
x3的圖象下方.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.
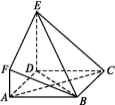
(1)求二面角F-BE-D的余弦值;
(2)設點M是線段BD上一個動點,試確定點M的位置,使得AM∥平面BEF,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右頂點為A,上頂點為B.已知橢圓的離心率為
的右頂點為A,上頂點為B.已知橢圓的離心率為![]() ,
,![]() .
.
(1)求橢圓的方程;
(2)設直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,
兩點,![]() 與直線
與直線![]() 交于點M,且點P,M均在第四象限.若
交于點M,且點P,M均在第四象限.若![]() 的面積是
的面積是![]() 面積的2倍,求
面積的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究機構對某校高二文科學生的記憶力x和判斷力y進行統計分析,得下表數據.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
參考公式: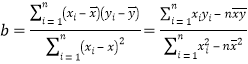
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是
A. 對分類變量X與Y,隨機變量K2的觀測值k越大,則判斷“X與Y有關系”的把握程度越小
B. 在回歸直線方程![]() =0.2x+0.8中,當解釋變量x每增加1個單位時,預報變量
=0.2x+0.8中,當解釋變量x每增加1個單位時,預報變量![]() 平均增加0.2個單位
平均增加0.2個單位
C. 兩個隨機變量的線性相關性越強,則相關系數的絕對值就越接近于1
D. 回歸直線過樣本點的中心(![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】人耳的聽力情況可以用電子測聽器檢測,正常人聽力的等級為0-25![]() (分貝),并規定測試值在區間
(分貝),并規定測試值在區間![]() 為非常優秀,測試值在區間
為非常優秀,測試值在區間![]() 為優秀.某班50名同學都進行了聽力測試,所得測試值制成頻率分布直方圖:
為優秀.某班50名同學都進行了聽力測試,所得測試值制成頻率分布直方圖:

(Ⅰ)現從聽力等級為![]() 的同學中任意抽取出4人,記聽力非常優秀的同學人數為
的同學中任意抽取出4人,記聽力非常優秀的同學人數為![]() ,求
,求![]() 的分布列與數學期望;
的分布列與數學期望;
(Ⅱ)在(Ⅰ)中抽出的4人中任選一人參加一個更高級別的聽力測試,測試規則如下:四個音叉的發生情況不同,由強到弱的次序分別為1,2,3,4.測試前將音叉隨機排列,被測試的同學依次聽完后給四個音叉按發音的強弱標出一組序號![]() ,
, ![]() ,
, ![]() ,
, ![]() (其中
(其中![]() ,
, ![]() ,
, ![]() ,
, ![]() 為1,2,3,4的一個排列).若
為1,2,3,4的一個排列).若![]() 為兩次排序偏離程度的一種描述,
為兩次排序偏離程度的一種描述, ![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com