
【題目】已知函數![]() ,其中函數
,其中函數![]() ,
,![]() .
.
(1)求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值;
上的最大值;
(3)當![]() 時,對于給定的正整數
時,對于給定的正整數![]() ,問:函數
,問:函數![]() 是否有零點?請說明理由.(參考數據
是否有零點?請說明理由.(參考數據![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)當
;(3)當![]() 時,函數
時,函數![]() 無零點;當
無零點;當![]() 時,函數
時,函數![]() 有零點,理由見解析.
有零點,理由見解析.
【解析】
(1)由導數可得切線斜率,進而由點斜式即可得切線方程;
(2)先求得![]() ,可得
,可得![]() 或
或![]() ,再比較
,再比較![]() 和
和![]() 的大小,利用函數單調性可得最大值;
的大小,利用函數單調性可得最大值;
(3)先證明![]() ,函數
,函數![]() 無零點,構造
無零點,構造![]() ,
,![]() ,利用
,利用![]() 可證得,
可證得,![]() ,函數
,函數![]() 有零點,利用零點存在性定理即可證得.
有零點,利用零點存在性定理即可證得.
(1)![]() ,故
,故![]() ,
,![]() ,∴切線方程為
,∴切線方程為![]() ,即
,即![]() .
.
(2)![]() ,
,![]() ,可得
,可得![]() 或
或![]() .
.
①![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,
∴![]() ;
;
②![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上遞增,
上遞增,![]() 遞減,在
遞減,在![]() 上遞增,
上遞增,
![]()
∴![]() ;
;
綜上所述,![]() ;
;
(3)![]() ,函數
,函數![]() 無零點,
無零點,
![]() ,函數
,函數![]() 有零點.
有零點.
理由如下:
![]() 時,證明
時,證明![]() 即可,即證明
即可,即證明![]() .
.
令![]() ,
,![]() ,
,
而![]() ,
,
令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,
![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
故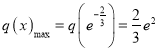 ,
,
∴![]() ,
,
故命題得證.
當![]() 時,
時,![]() ,
,
![]() ,
,![]() ,
,
所以![]() ,函數
,函數![]() 有零點.
有零點.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:只要
滿足:只要![]() ,必有
,必有![]() ,則稱
,則稱![]() 具有性質
具有性質![]() .
.
(1)若![]() 具有性質
具有性質![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若無窮數列![]() 是等差數列,無窮數列
是等差數列,無窮數列![]() 是等比數列,
是等比數列,![]() ,
,![]() ,
,![]() .判斷
.判斷![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(3)設![]() 是無窮數列,已知
是無窮數列,已知![]() .求證:“對任意
.求證:“對任意![]() 都具有性質
都具有性質![]() ”的充要條件為“
”的充要條件為“![]() 是常數列”.
是常數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘數學家阿波羅尼斯在其巨著《圓錐曲線論》中提出“在同一平面上給出三點,若其中一點到另外兩點的距離之比是一個大于零且不等于1的常數,則該點軌跡是一個圓”現在,某電信公司要在甲、乙、丙三地搭建三座5G信號塔來構建一個三角形信號覆蓋區域,以實現5G商用,已知甲、乙兩地相距4公里,丙、甲兩地距離是丙、乙兩地距離的![]() 倍,則這個三角形信號覆蓋區域的最大面積(單位:平方公里)是( )
倍,則這個三角形信號覆蓋區域的最大面積(單位:平方公里)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網購逐步走入百姓生活,網絡(電子)支付方面的股票受到一些股民的青睞.某單位4位熱愛炒股的好朋友研究后決定購買“生意寶”和“九州通“這兩支股票中的一支.他們約定:每人通過擲一枚質地均勻的骰子決定購買哪支股票,擲出點數為5或6的人買“九州通”股票,擲出點數為小于5的人買“生意寶”股票,且必須從“生意寶”和“九州通”這兩支股票中選擇一支股票購買.
(1)求這4人中恰有1人購買“九州通”股票的機率;
(2)用![]() ,
,![]() 分別表示這4人中購買“生意寶”和“九州通”股票的人數,記
分別表示這4人中購買“生意寶”和“九州通”股票的人數,記![]() ,求隨機變量X的分布列與數學期望
,求隨機變量X的分布列與數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】當前,以“立德樹人”為目標的課程改革正在有序推進. 高中聯招對初三畢業學生進行體育測試,是激發學生、家長和學校積極開展體育活動,保證學生健康成長的有效措施. 某地區2018年初中畢業生升學體育考試規定,考生必須參加立定跳遠、擲實心球、1分鐘跳繩三項測試,三項考試滿分為50分,其中立定跳遠15分,擲實心球15分,1分鐘跳繩20分. 某學校在初三上學期開始時要掌握全年級學生每分鐘跳繩的情況,隨機抽取了100名學生進行測試,得到右邊頻率分布直方圖,且規定計分規則如下表:
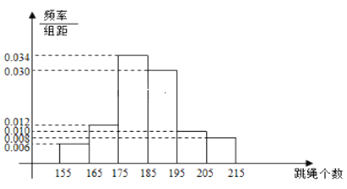

(1)現從樣本的100名學生中,任意選取2人,求兩人得分之和不大于33分的概率;
(2)若該校初三年級所有學生的跳繩個數![]() 服從正態分布
服從正態分布![]() ,用樣本數據的平均值和方差估計總體的期望和方差,已知樣本方差
,用樣本數據的平均值和方差估計總體的期望和方差,已知樣本方差![]() (各組數據用中點值代替). 根據往年經驗,該校初三年級學生經過一年的訓練,正式測試時每人每分鐘跳繩個數都有明顯進步,假設今年正式測試時每人每分鐘跳繩個數比初三上學期開始時個數增加10個,現利用所得正態分布模型:
(各組數據用中點值代替). 根據往年經驗,該校初三年級學生經過一年的訓練,正式測試時每人每分鐘跳繩個數都有明顯進步,假設今年正式測試時每人每分鐘跳繩個數比初三上學期開始時個數增加10個,現利用所得正態分布模型:
(ⅰ)預估全年級恰好有2000名學生時,正式測試每分鐘跳182個以上的人數;(結果四舍五入到整數)
(ⅱ)若在全年級所有學生中任意選取3人,記正式測試時每分鐘跳195個以上的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和期望. 附:若隨機變量
的分布列和期望. 附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() 在
在![]() 處取得最大值,求實數
處取得最大值,求實數![]() 的值;
的值;
(2)若![]() ,求
,求![]() 在區間
在區間![]() 上的最大值;
上的最大值;
(3)若![]() ,直線
,直線![]() 都不是曲線
都不是曲線![]() 的切線,求
的切線,求![]() 的取值范圍(只需直接寫出結果).
的取值范圍(只需直接寫出結果).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在高山滑雪運動的曲道賽項目中,運動員從高處(起點)向下滑,在滑行中運動員要穿過多個高約0.75米,寬4至6米的旗門,規定:運動員不經過任何一個旗門,都會被判一次“失格”,滑行時間會被增加,而所用時間越少,則排名越高.已知在參加比賽的運動員中,有五位運動員在滑行過程中都有三次“失格”,其中
(1)甲在滑行過程中依次沒有經過![]() ,
,![]() ,
,![]() 三個旗門;
三個旗門;
(2)乙在滑行過程中依次沒有經過![]() ,
,![]() ,
,![]() 三個旗門;
三個旗門;
(3)丙在滑行過程中依次沒有經過![]() ,
,![]() ,
,![]() 三個旗門;
三個旗門;
(4)丁在滑行過程中依次沒有經過![]() ,
,![]() ,
,![]() 三個旗門;
三個旗門;
(5)戊在滑行過程中依次沒有經過![]() ,
,![]() ,
,![]() 三個旗門.
三個旗門.
根據以上信息,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 這8個旗門從上至下的排列順序共有( )種可能.
這8個旗門從上至下的排列順序共有( )種可能.
A.6B.7C.8D.12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,側面
中,側面![]() 底面
底面![]() ,四邊形
,四邊形![]() 是邊長為2的菱形,
是邊長為2的菱形,![]() ,
,![]() ,
,![]() ,E,F分別為AC,
,E,F分別為AC,![]() 的中點.
的中點.

(1)求證:直線EF∥平面![]() ;
;
(2)設![]() 分別在側棱
分別在側棱![]() ,
,![]() 上,且
上,且![]() ,求平面BPQ分棱柱所成兩部分的體積比.
,求平面BPQ分棱柱所成兩部分的體積比.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com