
【題目】函數![]() ,
,![]() .
.
(1)求函數![]() 的單調區間及極值;
的單調區間及極值;
(2)若![]() ,
,![]() 是函數
是函數![]() 的兩個不同零點,求證:①
的兩個不同零點,求證:①![]() ;②
;②![]() .
.
【答案】(1)在![]() 遞減,
遞減,![]() 遞增,
遞增,![]() ,無極大值(2)見解析
,無極大值(2)見解析
【解析】分析:(1)求出![]() ,解不等式
,解不等式![]() 得增區間,解不等式
得增區間,解不等式![]() 得減區間,從而也可得到極值;
得減區間,從而也可得到極值;
(2)①先確定函數的變化趨勢,由函數式,知![]() 或
或![]() 時,都有
時,都有![]() ,從而要有兩個零點,則必有
,從而要有兩個零點,則必有![]() ,從而得
,從而得![]() .因此兩個零點
.因此兩個零點![]() ,不妨設
,不妨設![]() ,通過構造函數
,通過構造函數![]() ,由
,由![]() 的單調性可證
的單調性可證![]() ,即
,即![]() ,最后由
,最后由![]() 的單調性,得證
的單調性,得證![]() ,②證明:令
,②證明:令![]() ,然后證明
,然后證明![]() =
=![]() ,由
,由![]() ,得
,得![]() ,計算
,計算
![]() ,由
,由![]() 由
由![]() 得
得![]() ,再由
,再由![]() 在
在![]() 上的單調性可證結論.
上的單調性可證結論.
詳解:(1)定義域:![]()
![]()
令![]() ,則
,則![]() ,令
,令![]() ,則
,則![]()
∴![]() 在
在![]() 遞減,
遞減,![]() 遞增
遞增
∴![]() ,無極大值
,無極大值
(2)由(1)知![]() 時,
時,![]() ;
;![]() 時,
時,![]()
要使![]() 有兩個不同零點,則
有兩個不同零點,則![]() 即
即![]()
不妨設![]() ,
,
①證明:令![]() ,則
,則![]()
![]() 在
在![]() 遞增而
遞增而![]() ,∴
,∴![]()
∴![]() 即
即![]()
∵![]() ,∴
,∴![]()
∵![]() 且
且![]() 在
在![]() 遞減
遞減
∴![]() ,即
,即![]()
②證明:令![]() ,下面先證明
,下面先證明![]() ,
,![]()
∵![]() ,
,![]() ,∴
,∴![]() 在
在![]() 遞增
遞增
∴![]() ,∴
,∴![]() 在
在![]() 遞增,∴
遞增,∴![]()
即![]() 在
在![]() 總成立,∵
總成立,∵![]() ,∴
,∴![]()
又![]()
∵![]() 由
由![]() 知
知![]() ,
,![]()
又![]() ,
,![]() 且
且![]() 及
及![]() 在
在![]() 遞減
遞減
∴![]() ,即
,即![]()


科目:高中數學 來源: 題型:
【題目】中石化集團獲得了某地深海油田區塊的開采權,集團在該地區隨機初步勘探了部分兒口井,取得了地質資料.進入全面勘探時期后,集團按網絡點來布置井位進行全面勘探. 由于勘探一口井的費用很高,如果新設計的井位與原有井位重合或接近,便利用舊井的地質資料,不必打這口新井,以節約勘探費用.勘探初期數據資料見如表:

(Ⅰ)1~6號舊井位置線性分布,借助前5組數據求得回歸直線方程為![]() ,求
,求![]() ,并估計
,并估計![]() 的預報值;
的預報值;
(Ⅱ)現準備勘探新井![]() ,若通過1、3、5、7號井計算出的
,若通過1、3、5、7號井計算出的![]() 的值(
的值(![]() 精確到0.01)相比于(Ⅰ)中
精確到0.01)相比于(Ⅰ)中![]() 的值之差不超過10%,則使用位置最接近的已有舊井
的值之差不超過10%,則使用位置最接近的已有舊井![]() ,否則在新位置打開,請判斷可否使用舊井?
,否則在新位置打開,請判斷可否使用舊井?
(參考公式和計算結果: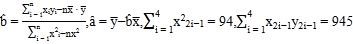 )
)
(Ⅲ)設出油量與勘探深度的比值![]() 不低于20的勘探并稱為優質井,那么在原有井號1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是優質井的概率.
不低于20的勘探并稱為優質井,那么在原有井號1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是優質井的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() ,直線
,直線![]() 設圓C的半徑為1,圓心在直線l上.
設圓C的半徑為1,圓心在直線l上.
(1)若圓心C也在直線![]() 上,過點
上,過點![]() 作圓C的切線,求切線的方程;
作圓C的切線,求切線的方程;
(2)若圓C上存在點M,使得![]() ,求圓心C的橫坐標
,求圓心C的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個正方形花圃被分成5份.

(1)若給這5個部分種植花,要求相鄰兩部分種植不同顏色的花,己知現有紅、黃、藍、綠4種顏色不同的花,求有多少種不同的種植方法?
(2)若向這5個部分放入7個不同的盆栽,要求每個部分都有盆栽,問有多少種不同的放法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,有下列四個命題:
,有下列四個命題:
①若![]() 是奇函數,則
是奇函數,則![]() 的圖象關于點
的圖象關于點![]() 對稱;
對稱;
②若對![]() ,有
,有![]() ,則
,則![]() 的圖象關于直線
的圖象關于直線![]() 對稱;
對稱;
③若對![]() ,有
,有![]() ,則
,則![]() 的圖象關于點
的圖象關于點![]() 對稱;
對稱;
④函數![]() 與函數
與函數![]() 的圖像關于直線
的圖像關于直線![]() 對稱.
對稱.
其中正確命題的序號為__________.(把你認為正確命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業2018年招聘員工,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五種崗位的應聘人數、錄用人數和錄用比例(精確到1%)如下:
五種崗位的應聘人數、錄用人數和錄用比例(精確到1%)如下:
崗位 | 男性 應聘人數 | 男性 錄用人數 | 男性 錄用比例 | 女性 應聘人數 | 女性 錄用人數 | 女性 錄用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
總計 | 533 | 264 |
| 467 | 169 |
|
(1)從表中所有應聘人員中隨機選擇1人,試估計此人被錄用的概率;
(2)從應聘![]() 崗位的6人中隨機選擇2人.記
崗位的6人中隨機選擇2人.記![]() 為這2人中被錄用的人數,求
為這2人中被錄用的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各崗位的男性、女性錄用比例都接近(二者之差的絕對值不大于
各崗位的男性、女性錄用比例都接近(二者之差的絕對值不大于![]() ),但男性的總錄用比例卻明顯高于女性的總錄用比例.研究發現,若只考慮其中某四種崗位,則男性、女性的總錄用比例也接近,請寫出這四種崗位.(只需寫出結論)
),但男性的總錄用比例卻明顯高于女性的總錄用比例.研究發現,若只考慮其中某四種崗位,則男性、女性的總錄用比例也接近,請寫出這四種崗位.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學團委組織了“弘揚奧運精神,愛我中華”的知識競賽,從參加考試的學生中抽出60名學生,將其成績(均為整數)分成六段[40,50),[50,60),…,[90,100]后畫出如下部分頻率分布直方圖.觀察圖形給出的信息,回答下列問題:

(1)求第四小組的頻率,并補全這個頻率分布直方圖;
(2)估計這次考試的及格率(60分及以上為及格)和平均分;
(3)從成績是[40,50)和[90,100]的學生中選兩人,求他們在同一分數段的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com