
【題目】隨著共享單車的蓬勃發展,越來越多的人將共享單車作為短距離出行的交通工具.為了解不同年齡的人們騎乘單車的情況,某共享單車公司對某區域不同年齡的騎乘者進行了調查,得到數據如下:
年齡 | 15 | 25 | 35 | 45 | 55 | 65 |
騎乘人數 | 95 | 80 | 65 | 40 | 35 | 15 |
(1)求![]() 關于
關于![]() 的線性回歸方程,并估計年齡為40歲人群的騎乘人數;
的線性回歸方程,并估計年齡為40歲人群的騎乘人數;
(2)為了回饋廣大騎乘者,該公司在五一當天通過![]() 向每位騎乘者的前兩次騎乘分別隨機派送一張面額為1元,或2元,或3元的騎行券.已知騎行一次獲得1元券,2元券,3元券的概率分別是
向每位騎乘者的前兩次騎乘分別隨機派送一張面額為1元,或2元,或3元的騎行券.已知騎行一次獲得1元券,2元券,3元券的概率分別是![]() ,
,![]() ,
,![]() ,且每次獲得騎行券的面額相互獨立.若一名騎乘者五一當天使用了兩次該公司的共享單車,記該騎乘者當天獲得的騎行券面額之和為
,且每次獲得騎行券的面額相互獨立.若一名騎乘者五一當天使用了兩次該公司的共享單車,記該騎乘者當天獲得的騎行券面額之和為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式:
 ,
,![]() .
.
參考數據:![]() ,
,![]() .
.
科目:高中數學 來源: 題型:
【題目】某企業響應省政府號召,對現有設備進行改造,為了分析設備改造前后的效果,現從設備改造前后生產的大量產品中各抽取了![]() 件產品作為樣本,檢測一項質量指標值,若該項質量指標值落在
件產品作為樣本,檢測一項質量指標值,若該項質量指標值落在![]() 內的產品視為合格品,否則為不合格品.如圖是設備改造前的樣本的頻率分布直方圖,表
內的產品視為合格品,否則為不合格品.如圖是設備改造前的樣本的頻率分布直方圖,表![]() 是設備改造后的樣本的頻數分布表.
是設備改造后的樣本的頻數分布表.
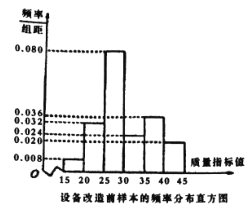
表:設備改造后樣本的頻數分布表
質量指標值 |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
(1)完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為該企業生產的這種產品的質量指標值與設備改造有關;
的把握認為該企業生產的這種產品的質量指標值與設備改造有關;
設備改造前 | 設備改造后 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
(2)根據頻率分布直方圖和表 提供的數據,試從產品合格率的角度對改造前后設備的優劣進行比較;
(3)企業將不合格品全部銷毀后,根據客戶需求對合格品進行登記細分,質量指標值落在![]() 內的定為一等品,每件售價
內的定為一等品,每件售價![]() 元;質量指標值落在
元;質量指標值落在![]() 或
或![]() 內的定為二等品,每件售價
內的定為二等品,每件售價![]() 元;其它的合格品定為三等品,每件售價
元;其它的合格品定為三等品,每件售價![]() 元.根據表
元.根據表![]() 的數據,用該組樣本中一等品、二等品、三等品各自在合格品中的頻率代替從所有產品中抽到一件相應等級產品的概率.現有一名顧客隨機購買兩件產品,設其支付的費用為
的數據,用該組樣本中一等品、二等品、三等品各自在合格品中的頻率代替從所有產品中抽到一件相應等級產品的概率.現有一名顧客隨機購買兩件產品,設其支付的費用為![]() (單位:元),求
(單位:元),求![]() 的分布列和數學期望.
的分布列和數學期望.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=lg(x+1)
(1)若0<f(1﹣2x)﹣f(x)<1,求x的取值范圍;
(2)若g(x)是以2為周期的偶函數,且當0≤x≤1時,g(x)=f(x),求函數y=g(x)(x∈[1,2])的反函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在邊長為6的正方形![]() 中,弧
中,弧![]() 的圓心為
的圓心為![]() ,過弧
,過弧![]() 上的點
上的點![]() 作弧
作弧![]() 的切線,與
的切線,與![]() 、
、![]() 分別相交于點
分別相交于點![]() 、
、![]() ,
,![]() 的延長線交
的延長線交![]() 邊于點
邊于點![]() .
.
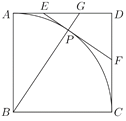
(1)設![]() ,
,![]() ,求
,求![]() 與
與![]() 之間的函數解析式,并寫出函數定義域;
之間的函數解析式,并寫出函數定義域;
(2)當![]() 時,求
時,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為提高員工的綜合素質,聘請專業機構對員工進行專業技術培訓,其中培訓機構費用成本為12000元.公司每位員工的培訓費用按以下方式與該機構結算:若公司參加培訓的員工人數不超過30人時,每人的培訓費用為850元;若公司參加培訓的員工人數多于30人,則給予優惠:每多一人,培訓費減少10元.已知該公司最多有60位員工可參加培訓,設參加培訓的員工人數為![]() 人,每位員工的培訓費為
人,每位員工的培訓費為![]() 元,培訓機構的利潤為
元,培訓機構的利潤為![]() 元.
元.
(1)寫出![]() 與
與![]()
![]() 之間的函數關系式;
之間的函數關系式;
(2)當公司參加培訓的員工為多少人時,培訓機構可獲得最大利潤?并求最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PD⊥平面ABCD,點E、F分別是AB和PC的中點.
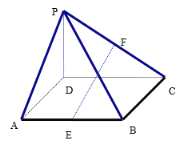
(1)求證:AB⊥平面PAD;
(2)求證:EF//平面PAD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com