
【題目】如圖,在斜三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,均為正三角形,E為AB的中點(diǎn).
,均為正三角形,E為AB的中點(diǎn).
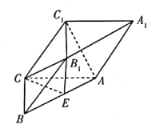
(1)證明:![]() 平面
平面![]() ,
,
(2)求直線(xiàn)![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見(jiàn)解析(2)![]()
【解析】
(1)如圖,連接![]() ,交
,交![]() 于點(diǎn)M,連接ME,則
于點(diǎn)M,連接ME,則![]() ,再利用線(xiàn)面平行的判定定理,即可證明線(xiàn)面平行;
,再利用線(xiàn)面平行的判定定理,即可證明線(xiàn)面平行;
(2)設(shè)O是AC的中點(diǎn),連接![]() ,OB,分別以射線(xiàn)OB,OA,
,OB,分別以射線(xiàn)OB,OA,![]() 的方向?yàn)?/span>x,y,z軸的正方向,建立空間直角坐標(biāo)系,求出平面
的方向?yàn)?/span>x,y,z軸的正方向,建立空間直角坐標(biāo)系,求出平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,設(shè)直線(xiàn)
,設(shè)直線(xiàn)![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,代入公式
,代入公式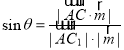 運(yùn)算,即可得答案.
運(yùn)算,即可得答案.
(1)如圖,連接![]() ,交
,交![]() 于點(diǎn)M,連接ME,則
于點(diǎn)M,連接ME,則![]() .
.
因?yàn)?/span>![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)設(shè)O是AC的中點(diǎn),連接![]() ,OB.因?yàn)?/span>
,OB.因?yàn)?/span>![]() 為正三角形,
為正三角形,
所以![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面ABC.由已知得
平面ABC.由已知得![]() .
.
如圖,分別以射線(xiàn)OB,OA,![]() 的方向?yàn)?/span>x,y,z軸的正方向,建立空間直角坐標(biāo)系,則有
的方向?yàn)?/span>x,y,z軸的正方向,建立空間直角坐標(biāo)系,則有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,![]() ,
,
設(shè)平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,則
,則 ,
,
所以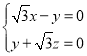 令
令![]() ,則
,則![]() .
.
設(shè)直線(xiàn)![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則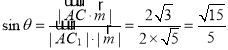 ,
,
故直線(xiàn)![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.



 小學(xué)生10分鐘口算測(cè)試100分系列答案
小學(xué)生10分鐘口算測(cè)試100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,一隧道內(nèi)設(shè)雙行線(xiàn)公路,其截面由一個(gè)長(zhǎng)方形和拋物線(xiàn)構(gòu)成.為保證安全,要求行使車(chē)輛頂部(設(shè)為平頂)與隧道頂部在豎直方向上的高度之差至少要有0.5米.若行車(chē)道總寬度AB為6米,則車(chē)輛通過(guò)隧道的限制高度是______米(精確到0.1米)

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知雙曲線(xiàn)![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,圓
,圓![]() 與雙曲線(xiàn)在第一象限內(nèi)的交點(diǎn)為M,若
與雙曲線(xiàn)在第一象限內(nèi)的交點(diǎn)為M,若![]() .則該雙曲線(xiàn)的離心率為
.則該雙曲線(xiàn)的離心率為
A. 2B. 3C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知集合![]() ,集合
,集合![]() ,
,![]() ,
,![]() 滿(mǎn)足.
滿(mǎn)足.
①每個(gè)集合都恰有5個(gè)元素
②![]()
![]()
![]()
集合![]() 中元素的最大值與最小值之和稱(chēng)為集合
中元素的最大值與最小值之和稱(chēng)為集合![]() 的特征數(shù),記為
的特征數(shù),記為![]() ,則
,則![]()
![]()
![]() 的值不可能為( )
的值不可能為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】國(guó)家統(tǒng)計(jì)局服務(wù)業(yè)調(diào)查中心和中國(guó)物流與采購(gòu)聯(lián)合會(huì)發(fā)布的2018年10月份至2019年9月份共12個(gè)月的中國(guó)制造業(yè)采購(gòu)經(jīng)理指數(shù)(PMI)如下圖所示.則下列結(jié)論中錯(cuò)誤的是( )
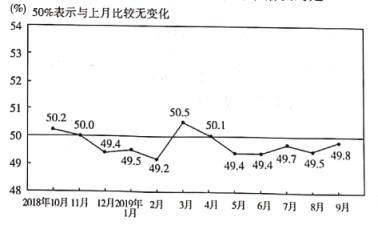
A.12個(gè)月的PMI值不低于50%的頻率為![]()
B.12個(gè)月的PMI值的平均值低于50%
C.12個(gè)月的PMI值的眾數(shù)為49.4%
D.12個(gè)月的PMI值的中位數(shù)為50.3%
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上的函數(shù),滿(mǎn)足
上的函數(shù),滿(mǎn)足 .
.
(1)證明:2是函數(shù)![]() 的周期;
的周期;
(2)當(dāng)![]() 時(shí),
時(shí),![]() ,求
,求![]() 在
在![]() 時(shí)的解析式,并寫(xiě)出
時(shí)的解析式,并寫(xiě)出![]() 在
在![]() (
(![]() )時(shí)的解析式;
)時(shí)的解析式;
(3)對(duì)于(2)中的函數(shù)![]() ,若關(guān)于x的方程
,若關(guān)于x的方程![]() 恰好有20個(gè)解,求實(shí)數(shù)a的取值范圍.
恰好有20個(gè)解,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】《算法統(tǒng)宗》全稱(chēng)《新編直指算法統(tǒng)宗》,是屮國(guó)古代數(shù)學(xué)名著,程大位著.書(shū)中有如下問(wèn)題:“今有五人均銀四十兩,甲得十兩四錢(qián),戊得五兩六錢(qián).問(wèn):次第均之,乙丙丁各該若干?”意思是:有5人分40兩銀子,甲分10兩4錢(qián),戊分5兩6錢(qián),且相鄰兩項(xiàng)差相等,則乙丙丁各分幾兩幾錢(qián)?(注:1兩等于10錢(qián))( )
A.乙分8兩,丙分8兩,丁分8兩B.乙分8兩2錢(qián),丙分8兩,丁分7兩8錢(qián)
C.乙分9兩2錢(qián),丙分8兩,丁分6兩8錢(qián)D.乙分9兩,丙分8兩,丁分7兩
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某基地蔬菜大棚采用水培、無(wú)土栽培方式種植各類(lèi)蔬菜.過(guò)去50周的資料顯示,該地周光照量![]() (小時(shí))都在30小時(shí)以上,其中不足50小時(shí)的周數(shù)有5周,不低于50小時(shí)且不超過(guò)70小時(shí)的周數(shù)有35周,超過(guò)70小時(shí)的周數(shù)有10周.根據(jù)統(tǒng)計(jì),該基地的西紅柿增加量
(小時(shí))都在30小時(shí)以上,其中不足50小時(shí)的周數(shù)有5周,不低于50小時(shí)且不超過(guò)70小時(shí)的周數(shù)有35周,超過(guò)70小時(shí)的周數(shù)有10周.根據(jù)統(tǒng)計(jì),該基地的西紅柿增加量![]() (百斤)與使用某種液體肥料
(百斤)與使用某種液體肥料![]() (千克)之間對(duì)應(yīng)數(shù)據(jù)為如圖所示的折線(xiàn)圖.
(千克)之間對(duì)應(yīng)數(shù)據(jù)為如圖所示的折線(xiàn)圖.

(1)依據(jù)數(shù)據(jù)的折線(xiàn)圖,是否可用線(xiàn)性回歸模型擬合![]() 與
與![]() 的關(guān)系?請(qǐng)計(jì)算相關(guān)系數(shù)
的關(guān)系?請(qǐng)計(jì)算相關(guān)系數(shù)![]() 并加以說(shuō)明(精確到0.01).(若
并加以說(shuō)明(精確到0.01).(若![]() ,則線(xiàn)性相關(guān)程度很高,可用線(xiàn)性回歸模型擬合)
,則線(xiàn)性相關(guān)程度很高,可用線(xiàn)性回歸模型擬合)
(2)蔬菜大棚對(duì)光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀最多可運(yùn)行臺(tái)數(shù)受周光照量![]() 限制,并有如下關(guān)系:
限制,并有如下關(guān)系:
周光照量 |
|
|
|
光照控制儀最多可運(yùn)行臺(tái)數(shù) | 3 | 2 | 1 |
若某臺(tái)光照控制儀運(yùn)行,則該臺(tái)光照控制儀周利潤(rùn)為3000元;若某臺(tái)光照控制儀未運(yùn)行,則該臺(tái)光照控制儀周虧損1000元.若商家安裝了3臺(tái)光照控制儀,求商家在過(guò)去50周周總利潤(rùn)的平均值.
附:相關(guān)系數(shù)公式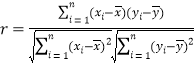 ,參考數(shù)據(jù)
,參考數(shù)據(jù)![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,三棱柱![]() 中,
中,![]() 側(cè)面
側(cè)面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,點(diǎn)E是棱
,點(diǎn)E是棱![]() 的中點(diǎn).
的中點(diǎn).

(1)求證:![]() 平面ABC;
平面ABC;
(2)在棱CA上是否存在一點(diǎn)M,使得EM與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com