
【題目】設(shè)函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)有兩個零點,求滿足條件的最小正整數(shù)![]() 的值.
的值.
【答案】(1) 當![]() 時,
時,![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ;當
;當![]() 時,
時,![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]() ;(2)3.
;(2)3.
【解析】
(1)先求導,再對![]() 進行分類討論,利用導數(shù)與函數(shù)的單調(diào)性的關(guān)系即可得出;
進行分類討論,利用導數(shù)與函數(shù)的單調(diào)性的關(guān)系即可得出;
(2)由(1)可知,若函數(shù)![]() 有兩個零點,則
有兩個零點,則![]() ,且
,且![]() .轉(zhuǎn)化為求滿足
.轉(zhuǎn)化為求滿足![]() 的最小正整數(shù)
的最小正整數(shù)![]() 的值,利用單調(diào)性判斷其零點所在的最小區(qū)間即可求得.
的值,利用單調(diào)性判斷其零點所在的最小區(qū)間即可求得.
(1)函數(shù)![]() 的定義域為
的定義域為![]() .
.
![]() .
.
![]() ,
,
![]() 當
當![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當![]() 時,由
時,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .所以函數(shù)
.所以函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
綜上所述,當![]() 時,
時,![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ;
;
當![]() 時,
時,![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]() .
.
(2)由(1)可知,若函數(shù)![]() 有兩個零點,則
有兩個零點,則![]() ,且
,且![]() .
.
即 ,
,
即![]() ,
,
![]() .
.
令![]() ,易知
,易知![]() 在
在![]() 上是增函數(shù),且
上是增函數(shù),且![]() ,
,
又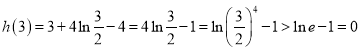 ,
,
即![]() .
.
所以存在![]() ,使
,使![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以滿足![]() 的最小正整數(shù)
的最小正整數(shù)![]() 的值為3.
的值為3.
又![]() 時,
時,![]() ,且函數(shù)
,且函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
![]() 時,函數(shù)
時,函數(shù)![]() 有兩個零點.
有兩個零點.
綜上,滿足條件的最小正整數(shù)![]() 的值為3.
的值為3.


科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形,![]() 平面
平面![]() ,
,![]() ,點
,點![]() 分別為
分別為![]() 的中點.
的中點.
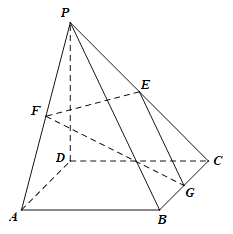
(Ⅰ)求證:![]() ;
;
(Ⅱ)求證:![]()
![]() 平面
平面![]() ;
;
(Ⅲ)求平面![]() 與平面
與平面![]() 所成二面角
所成二面角![]() (銳角)的余弦值.
(銳角)的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
![]() ,函數(shù)
,函數(shù)![]()
⑴當![]() 時,求函數(shù)
時,求函數(shù)![]() 的表達式;
的表達式;
⑵若![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上的最小值是2 ,求
上的最小值是2 ,求![]() 的值;
的值;
⑶在⑵的條件下,求直線![]()
![]() 與函數(shù)
與函數(shù)![]() 的圖象所圍成圖形的面積.
的圖象所圍成圖形的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若對任意![]() ,都有
,都有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若存在![]() ,使
,使![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若對任意![]() ,都有
,都有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】現(xiàn)拋擲兩枚骰子,記事件![]() 為“朝上的2個數(shù)之和為偶數(shù)”,事件
為“朝上的2個數(shù)之和為偶數(shù)”,事件![]() 為“朝上的2個數(shù)均為偶數(shù)”,則
為“朝上的2個數(shù)均為偶數(shù)”,則![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐E﹣ABCD的側(cè)棱DE與四棱錐F﹣ABCD的側(cè)棱BF都與底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
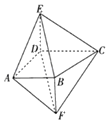
(1)證明:![]() //平面BCE.
//平面BCE.
(2)設(shè)平面ABF與平面CDF所成的二面角為θ,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為認真貫徹落實黨中央國務(wù)院決策部署,堅持“房子是用來住的,不是用來炒的”定位,堅持調(diào)控政策的連續(xù)性和穩(wěn)定性,進一步穩(wěn)定某省市商品住房市場,該市人民政府辦公廳出臺了相關(guān)文件來控制房價,并取得了一定效果,下表是2019年2月至6月以來該市某城區(qū)的房價均值數(shù)據(jù):
| 2 | 3 | 4 | 5 | 6 |
| 9.80 | 9.70 |
| 9.30 | 9.20 |
已知:![]() .
.![]()
(1)若變量![]() 、
、![]() 具有線性相關(guān)關(guān)系,求房價均價
具有線性相關(guān)關(guān)系,求房價均價![]() (千元/平方米)關(guān)于月份
(千元/平方米)關(guān)于月份![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)根據(jù)線性回歸方程預測該市某城區(qū)7月份的房價.
(參考公式:用最小二乘法求線性回歸方程![]() 的系數(shù)公式
的系數(shù)公式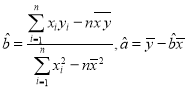 )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
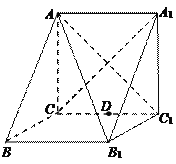
【題目】如圖所示,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)證明:![]()
![]() 平面
平面![]() ;
;
(2)若![]() 是棱
是棱![]() 的中點,在棱
的中點,在棱![]() 上是否存在一點
上是否存在一點![]() ,使DE∥平面
,使DE∥平面![]() ?證明你的結(jié)論.
?證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
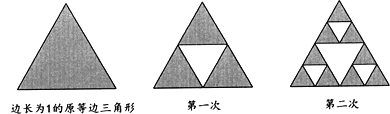
【題目】如圖,將一個邊長為![]() 的正三角形分成
的正三角形分成![]() 個全等的正三角形,第一次挖去中間的一個小三角形,將剩下的
個全等的正三角形,第一次挖去中間的一個小三角形,將剩下的![]() 個小正三角形,分別再從中間挖去一個小三角形,保留它們的邊,重復操作以上的做法,得到的集合為希爾賓斯基三角形.設(shè)
個小正三角形,分別再從中間挖去一個小三角形,保留它們的邊,重復操作以上的做法,得到的集合為希爾賓斯基三角形.設(shè)![]() 是前
是前![]() 次挖去的小三角形面積之和(如
次挖去的小三角形面積之和(如![]() 是第
是第![]() 次挖去的中間小三角形面積,
次挖去的中間小三角形面積,![]() 是前
是前![]() 次挖去的
次挖去的![]() 個小三角形面積之和),則
個小三角形面積之和),則![]() _____________ ,
_____________ ,![]() __________.
__________.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com