
【題目】已知函數f(x)=x3﹣ ![]() ax2 , 且關于x的方程f(x)+a=0有三個不等的實數根,則實數a的取值范圍是( )
ax2 , 且關于x的方程f(x)+a=0有三個不等的實數根,則實數a的取值范圍是( )
A.(﹣∞,﹣ ![]() )∪(0,
)∪(0, ![]() )
)
B.(﹣ ![]() ,0)∪(
,0)∪( ![]() ,+∞)
,+∞)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
【答案】D
【解析】解:令g(x)=f(x)+a=x3﹣ ![]() ax2+a,
ax2+a,
得g′(x)=3x2﹣3ax=3x(x﹣a),
當a=0時,g′(x)≥0,函數g(x)為增函數,不合題意;
當a<0時,x∈(﹣∞,a),(0,+∞)時,g′(x)>0;x∈(a,0)時,g′(x)<0.
∴x∈(﹣∞,a),(0,+∞)時,g(x)單調遞增;x∈(a,0)時,g(x)單調遞減,
∴x=a時函數有極大值為g(a)= ![]() ,x=0時函數有極小值為g(0)=a.
,x=0時函數有極小值為g(0)=a.
由 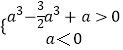 ,解得a
,解得a ![]() ;
;
當a>0時,x∈(﹣∞,0),(a,+∞)時,g′(x)>0;x∈(0,a)時,g′(x)<0.
∴x∈(﹣∞,0),(a,+∞)時,g(x)單調遞增;x∈(0,a)時,g(x)單調遞減,
∴x=0時函數有極大值為g(0)=a,x=a時函數有極小值為g(a)= ![]() .
.
由 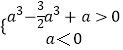 ,解得a
,解得a ![]() .
.
綜上,實數a的取值范圍是(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞).
,+∞).
故選:D.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是定義在R上的增函數,函數y=f(x﹣1)的圖象關于(1,0)對稱.若對任意的x,y∈R,不等式f(x2﹣6x+21)+f(y2﹣8y)<0恒成立,則當x>3時,x2+y2的取值范圍是( )
A.(9,25)
B.(13,49)
C.(3,7)
D.(9,49)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲罐中有4個紅球,3個白球和3個黑球;乙罐中有5個紅球,3個白球和2個黑球.先從甲罐中隨機取出一球放入乙罐,分別以A1、A2和A3表示由甲罐取出的球是紅球,白球和黑球的事件;再從乙罐中隨機取出一球,以B表示由乙罐取出的球是紅球的事件,下列的結論:
①P(B)= ![]() ;
;
②P(B|A1)= ![]() ;
;
③事件B與事件A1不相互獨立;
④A1 , A2 , A3是兩兩互斥的事件;
⑤P(B)的值不能確定,因為它與A1 , A2 , A3中哪一個發生有關,
其中正確結論的序號為 . (把正確結論的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】梯形ABCD頂點B、C在以AD為直徑的圓上,AD=2米,
(1)如圖1,若電熱絲由AB,BC,CD這三部分組成,在AB,CD上每米可輻射1單位熱量,在BC上每米可輻射2單位熱量,請設計BC的長度,使得電熱絲輻射的總熱量最大,并求總熱量的最大值;
(2)如圖2,若電熱絲由弧![]() 和弦BC這三部分組成,在弧
和弦BC這三部分組成,在弧![]() 上每米可輻射1單位熱量,在弦BC上每米可輻射2單位熱量,請設計BC的長度,使得電熱絲輻射的總熱量最大.
上每米可輻射1單位熱量,在弦BC上每米可輻射2單位熱量,請設計BC的長度,使得電熱絲輻射的總熱量最大.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ex(ax+b)(其中e=2.71828…),g(x)=x2+2bx+2,已知它們在x=0處有相同的切線.
(1)求函數f(x),g(x)的解析式;
(2)若函數F(x)=f(x)+g(x)﹣2(ex+x),試判斷函數F(x)的零點個數,并說明理由;
(3)若函數f(x)在[t,t+1](t>﹣3)上的最小值為φ(t),解關于t的不等式φ(t)≤4e2 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了檢驗學習情況,某培訓機構于近期舉辦一場競賽活動,分別從甲、乙兩班各抽取10名學員的成績進行統計分析,其成績的莖葉圖如圖所示(單位:分),假設成績不低于90分者命名為“優秀學員”.
(1)分別求甲、乙兩班學員成績的平均分(結果保留一位小數);
(2)從甲班4名優秀學員中抽取兩人,從乙班2名80分以下的學員中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為宣傳3月5日學雷鋒紀念日,重慶二外在高一,高二年級中舉行學雷鋒知識競賽,每年級出3人組成甲乙兩支代表隊,首輪比賽每人一道必答題,答對則為本隊得1分,答錯不答都得0分,已知甲隊3人每人答對的概率分別為![]() ,乙隊每人答對的概率都是
,乙隊每人答對的概率都是![]() .設每人回答正確與否相互之間沒有影響,用
.設每人回答正確與否相互之間沒有影響,用![]() 表示甲隊總得分.
表示甲隊總得分.
(1)求隨機變量![]() 的分布列及其數學期望
的分布列及其數學期望![]() ;
;
(2)求甲隊和乙隊得分之和為4的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=cos(x+ ![]() )圖象上所有點的橫坐標縮短為原來的
)圖象上所有點的橫坐標縮短為原來的 ![]() 倍,縱坐標不變,得到函數g(x)的圖象,則函數g(x)的一個減區間是( )
倍,縱坐標不變,得到函數g(x)的圖象,則函數g(x)的一個減區間是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com