
【題目】在直角坐標系xOy中,直線l的參數方程為![]() ,(t為參數),在以坐標原點為極點,x軸正半軸為極軸的極坐標系中,曲線C1:ρ=2cosθ,
,(t為參數),在以坐標原點為極點,x軸正半軸為極軸的極坐標系中,曲線C1:ρ=2cosθ,![]() .
.
(1)求C1與C2交點的直角坐標;
(2)若直線l與曲線C1,C2分別相交于異于原點的點M,N,求|MN|的最大值.
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,側面
中,側面![]() 底面
底面![]() ,四邊形
,四邊形![]() 是邊長為2的菱形,
是邊長為2的菱形,![]() ,
,![]() ,
,![]() ,E,F分別為AC,
,E,F分別為AC,![]() 的中點.
的中點.

(1)求證:直線EF∥平面![]() ;
;
(2)設![]() 分別在側棱
分別在側棱![]() ,
,![]() 上,且
上,且![]() ,求平面BPQ分棱柱所成兩部分的體積比.
,求平面BPQ分棱柱所成兩部分的體積比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著科技的發展,網絡已逐漸融入了人們的生活.網購是非常方便的購物方式,為了了解網購在我市的普及情況,某調查機構進行了有關網購的調查問卷,并從參與調查的市民中隨機抽取了男女各100人進行分析,從而得到表(單位:人)
經常網購 | 偶爾或不用網購 | 合計 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合計 |
(1)完成上表,并根據以上數據判斷能否在犯錯誤的概率不超過0.01的前提下認為我市市民網購與性別有關?
(2)①現從所抽取的女市民中利用分層抽樣的方法抽取10人,再從這10人中隨機選取3人贈送優惠券,求選取的3人中至少有2人經常網購的概率;
②將頻率視為概率,從我市所有參與調查的市民中隨機抽取10人贈送禮品,記其中經常網購的人數為![]() ,求隨機變量
,求隨機變量![]() 的數學期望和方差.
的數學期望和方差.
參考公式: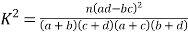
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知空間中不同直線m、n和不同平面α、β,下面四個結論:
①若m、n互為異面直線,m∥α,n∥α,m∥β,n∥β,則α∥β;
②若m⊥n,m⊥α,n∥β,則α⊥β;
③若n⊥α,m∥α,則n⊥m;
④若α⊥β,m⊥α,n∥m,則n∥β.
其中正確的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的上頂點為
)的上頂點為![]() ,左焦點為
,左焦點為![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 與圓
與圓![]() 相切.
相切.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過點![]() 且斜率存在的直線
且斜率存在的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,線段
兩點,線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點
軸于點![]() ,試判斷
,試判斷![]() 是否為定值?并說明理由.
是否為定值?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為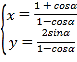 (
(![]() 為參數).以
為參數).以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ),將曲線
),將曲線![]() 向左平移2個單位長度得到曲線
向左平移2個單位長度得到曲線![]() .
.
(1)求曲線![]() 的普通方程和極坐標方程;
的普通方程和極坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“偉大的變革—慶祝改革開放40周年大型展覽”于2019年3月20日在中國國家博物館閉幕,本次特展緊扣“改革開放40年光輝歷程”的主線,多角度、全景式描繪了我國改革開放40年波瀾壯闊的歷史畫卷.據統計,展覽全程呈現出持續火爆的狀態,現場觀眾累計達423萬人次,參展人數屢次創造國家博物館參觀紀錄,網上展館點擊瀏覽總量達4.03億次.
下表是2019年2月參觀人數(單位:萬人)統計表
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
人數 | 3.0 | 3.1 | 2.5 | 2.3 | 5.4 | 6.8 | 6.2 | 6.7 | 5.5 | 4.9 | 3.2 | 3.0 | 2.7 | 2.5 |
日期 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
人數 | 2.4 | 2.9 | 3.2 | 2.8 | 2.9 | 2.3 | 3.0 | 2.9 | 3.1 | 3.0 | 3.1 | 3.1 | 3.1 | 3.0 |
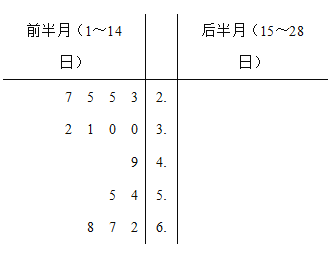
根據表中數據回答下列問題:
(1)請將2019年2月前半月(1~14日)和后半月(15~28日)參觀人數統計對比莖葉圖填補完整,并通過莖葉圖比較兩組數據方差的大小(不要求計算出具體值,得出結論即可);
(2)將2019年2月參觀人數數據用該天的對應日期作為樣本編號,現從中抽樣7天的樣本數據.若抽取的樣本編號是以4為公差的等差數列,且數列的第4項為15,求抽出的這7個樣本數據的平均值;
(3)根據國博以往展覽數據及調查統計信息可知,單日入館參觀人數為0~3(含3,單位:萬人)時,參觀者的體驗滿意度最佳,在從(2)中抽出的樣本數據中隨機抽取兩天的數據,求這兩天參觀者的體驗滿意度均為最住的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 的最大值為
的最大值為![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(Ⅲ)當![]() 時,令
時,令![]() ,是否存在區間
,是否存在區間![]() .使得函數
.使得函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() 若存在,求實數
若存在,求實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com