
【題目】《中國詩詞大會》是由CCTV-10自主研發的一檔大型文化益智節目,以“賞中華詩詞,尋文化基因品生活之美”為宗旨,帶動全民重溫經典、從古人的智慧和情懷中汲取營養、涵養心靈,節目廣受好評還因為其頗具新意的比賽規則:每場比賽,106位挑戰者全部參賽,分為單人追逐賽和擂主爭霸賽兩部分單人追逐賽的最終優勝者作為攻擂者與守擂擂主進行比拼,競爭該場比賽的擂主,擂主爭霸賽以搶答的形式展開,共九道題,搶到并回答正確者得一分,答錯則對方得一分,先得五分者獲勝,成為本場擂主,比賽結束已知某場擂主爭霸賽中,攻擂者與守擂擂主都參與每一次搶題且兩人搶到每道題的概率都是![]() ,攻擂者與守擂擂主正確回答每道題的概率分別為
,攻擂者與守擂擂主正確回答每道題的概率分別為![]() ,
,![]() ,且兩人各道題是否回答正確均相互獨立.
,且兩人各道題是否回答正確均相互獨立.
(1)比賽開始,求攻擂者率先得一分的概率;
(2)比賽進行中,攻擂者暫時以![]() 領先,設兩人共繼續搶答了
領先,設兩人共繼續搶答了![]() 道題比賽結束,求隨機變量
道題比賽結束,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
【答案】(1)![]() (2)答案見解析
(2)答案見解析
【解析】
(1)由題意可知:每道題的搶答中,記攻擂者得一分為事件![]() ,
,![]() 發生有兩種可能:搶到題且答對,對方搶到題且答錯,即可求得攻擂者率先得一分的概率;
發生有兩種可能:搶到題且答對,對方搶到題且答錯,即可求得攻擂者率先得一分的概率;
(2)由(1)知,在每道題的搶答中攻擂者與守擂擂主得一分的概率分別為![]() ,
,![]() .根據比賽規則,
.根據比賽規則,![]() 的所有可能取值分別為
的所有可能取值分別為![]() ,求出
,求出![]() ,
,![]() 和
和![]() ,即可求得隨機變量
,即可求得隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
(1)每道題的搶答中,記攻擂者得一分為事件![]() .
.
![]() 發生有兩種可能:搶到題且答對,對方搶到題且答錯,
發生有兩種可能:搶到題且答對,對方搶到題且答錯,
![]()
![]()
![]() 比賽開始,求攻擂者率先得一分的概率為:
比賽開始,求攻擂者率先得一分的概率為:![]() .
.
(2)由(1)知,在每道題的搶答中攻擂者與守擂擂主得一分的概率分別為![]() ,
,![]()
根據比賽規則,![]() 的所有可能取值分別為
的所有可能取值分別為![]() ,
,
則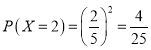
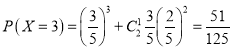
![]()
![]() 的分布列為:
的分布列為:
| 2 | 3 | 4 |
|
|
|
|
![]()
![]() .
.


科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代內容極為豐富的數學名著,書中有一個“引葭赴岸”問題:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,適與岸齊.問水深、葭長各幾何?”其意思為“今有水池1丈見方(即![]() 尺),蘆葦生長在水的中央,長出水面的部分為1尺.將蘆葦向池岸牽引,恰巧與水岸齊接(如圖所示).試問水深、蘆葦的長度各是多少?假設
尺),蘆葦生長在水的中央,長出水面的部分為1尺.將蘆葦向池岸牽引,恰巧與水岸齊接(如圖所示).試問水深、蘆葦的長度各是多少?假設![]() ,現有下述四個結論:
,現有下述四個結論:
①水深為12尺;②蘆葦長為15尺;③![]() ;④
;④![]() .
.
其中所有正確結論的編號是( )
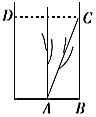
A.①③B.①③④C.①④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國在2018年社保又出新的好消息,之前流動就業人員跨地區就業后,社保轉移接續的手續往往比較繁瑣,費時費力.社保改革后將簡化手續,深得流動就業人員的贊譽.某市社保局從2018年辦理社保的人員中抽取300人,得到其辦理手續所需時間(天)與人數的頻數分布表:
時間 |
|
|
|
|
|
|
人數 | 15 | 60 | 90 | 75 | 45 | 15 |
(1)若300名辦理社保的人員中流動人員210人,非流動人員90人,若辦理時間超過4天的人員里非流動人員有60人,請完成辦理社保手續所需時間與是否流動人員的列聯表,并判斷是否有95%的把握認為“辦理社保手續所需時間與是否流動人員”有關.
列聯表如下
流動人員 | 非流動人員 | 總計 | |
辦理社保手續所需 時間不超過4天 | |||
辦理社保手續所需 時間超過4天 | 60 | ||
總計 | 210 | 90 | 300 |
(2)為了改進工作作風,提高效率,從抽取的300人中辦理時間為![]() 流動人員中利用分層抽樣,抽取12名流動人員召開座談會,其中3人要求交書面材料,3人中辦理的時間為
流動人員中利用分層抽樣,抽取12名流動人員召開座談會,其中3人要求交書面材料,3人中辦理的時間為![]() 的人數為
的人數為![]() ,求出
,求出![]() 分布列及期望值.
分布列及期望值.
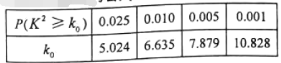
附: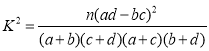
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,左、右頂點分別為
,左、右頂點分別為![]() 、
、![]() ,過左焦點的直線
,過左焦點的直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點(異于
兩點(異于![]() 、
、![]() 兩點),當直線
兩點),當直線![]() 垂直于
垂直于![]() 軸時,四邊形
軸時,四邊形![]() 的面積為6.
的面積為6.
(1)求橢圓的方程;
(2)設直線![]() 、
、![]() 的交點為
的交點為![]() ;試問
;試問![]() 的橫坐標是否為定值?若是,求出定值;若不是,請說明理由.
的橫坐標是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(1,![]() )是離心率為
)是離心率為![]() 的橢圓C:
的橢圓C:![]() (a>b>0)上的一點,斜率為
(a>b>0)上的一點,斜率為![]() 的直線BD交橢圓C于B、D兩點,且A、B、D三點不重合
的直線BD交橢圓C于B、D兩點,且A、B、D三點不重合
(1)求橢圓C的方程;
(2)求證:直線AB,AD的斜率之和為定值
(3)△ABD面積是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位共有職工2000人,其中男職工1200人,女職工800人為調查2019年“雙十一”購物節的消費情況,按照性別采用分層抽樣的方法抽取了該單位100人在“雙十一”當天網絡購物的消費金額(單位:百元),其頻率分布直方圖如下:

(1)已知抽取的樣本中,有3名女職工的消費不低于1000元,現從消費不低于1000元的職工中抽取3名職工進行購物指導,求抽取的3名職工中至少有兩名女職工的概率;
(2)在“雙十一”當天網絡購物消費金額不低于600元者稱為“購物狂”,低于600元者稱為“理性購物者”.已知在抽取的樣本中有18名女職工消費不低于600元,請完成上圖中的列聯表,并判斷能否有99%的把握認為“是不是購物狂”與性別有關.
附:參考數據與公式
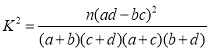
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若曲線![]() 在
在![]() 處的切線恰與曲線
處的切線恰與曲線![]() 相切,求a的值;
相切,求a的值;
(2)不等式![]() 對一切正實數x恒成立,求a的取值范圍;
對一切正實數x恒成立,求a的取值范圍;
(3)已知![]() ,若函數
,若函數![]() 在
在![]() 上有且只有一個零點,求a的取值范圍.
上有且只有一個零點,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《孫子算經》是中國古代重要的數學著作,書中有一問題:“今有方物一束,外周一匝有三十二枚,問積幾何?”,該著作中提出了一種解決此問題的方法:“重置二位,左位減八,余加右位,至盡虛減一,即得.”通過對該題的研究發現,若一束方物外周一匝的枚數![]() 是8的整數倍時,均可采用此方法求解,如圖是解決這類問題的程序框圖,若輸入
是8的整數倍時,均可采用此方法求解,如圖是解決這類問題的程序框圖,若輸入![]() ,則輸出的結果為( )
,則輸出的結果為( )
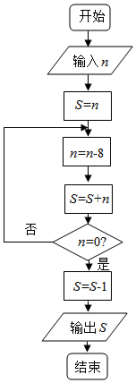
A.80B.47C.79D.48
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代有著輝煌的數學研究成果,其中《周髀算經》、《九章算術》、《海島算經》、《孫子算經》、《緝古算經》有著豐富多彩的內容,是了解我國古代數學的重要文獻.這5部專著中有3部產生于漢、魏、晉、南北朝時期.現擬從這5部專著中選擇2部作為學生課外興趣拓展參考書目,則所選2部專著中至少有一部不是漢、魏、晉、南北朝時期專著的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com