
(本大題滿分12分)
某公司預計全年分批購入每臺價值為2 000元的電視機共3600臺,每批都購入x臺
000元的電視機共3600臺,每批都購入x臺 ,且每批均需付運費400元,儲存購入的電視機全年所付保管費與每批購入電視機的總價值(不含運費)成正比。若每批購入400臺,則全年需用去運費和保管費43600元。現在全年只有24000元資金用于支付運費和保管費,請問能否恰
,且每批均需付運費400元,儲存購入的電視機全年所付保管費與每批購入電視機的總價值(不含運費)成正比。若每批購入400臺,則全年需用去運費和保管費43600元。現在全年只有24000元資金用于支付運費和保管費,請問能否恰 當安排每批進貨的數量,使資金夠用?寫出你的結論并說明理由
當安排每批進貨的數量,使資金夠用?寫出你的結論并說明理由
科目:高中數學 來源: 題型:解答題
(本題滿分16分)
已知函數 (
( ∈R且
∈R且 ),
), .
.
(Ⅰ)若 ,且函數
,且函數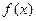 的值域為[0, +
的值域為[0, + ),求
),求 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的條件下,當x∈[-2 , 2 ]時, 是單調函數,求實數k的取值范圍;
是單調函數,求實數k的取值范圍;
(Ⅲ)設 ,
, , 且
, 且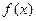 是偶函數,判斷
是偶函數,判斷 能否大于零?
能否大于零?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(滿分16分)
記函數f(x)的定義域為D,若存在 ,使
,使 成立,則稱以
成立,則稱以 為坐標的點為函數
為坐標的點為函數 圖象上的不動點。
圖象上的不動點。
(1)若函數 的圖象上有兩個關于原點對稱的不動點,求
的圖象上有兩個關于原點對稱的不動點,求 應滿足的條件;
應滿足的條件;
(2)下述結論“若定義在R上的奇函數f(x)的圖象上存在有限個不動點,則不動點有奇數個”是否正確?若正確,請給予證明,并舉出一例;若不正確,請舉出一反例說明
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)若實數 、
、 、
、 滿足
滿足 ,則稱
,則稱 比
比 接近
接近 .
.
(1)若 比3接近0,求
比3接近0,求 的取值范圍;
的取值范圍;
(2)對任意兩個不相等的正數 、
、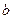 ,證明:
,證明: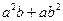 比
比 接近
接近 ;
;
(3)已知函數 的定義域
的定義域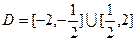 .任取
.任取 ,
, 等于
等于 和
和 中接近0的那個值.寫出函數
中接近0的那個值.寫出函數 的解析式,并指出它的奇偶性、最值和單調性(結論不要求證明).
的解析式,并指出它的奇偶性、最值和單調性(結論不要求證明).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)
已知函數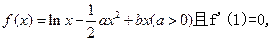
(I)試用含a的式子表示b,并求函數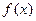 的單調區間;
的單調區間;
(II)已知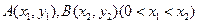 為函數
為函數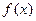 圖象上不同兩點,
圖象上不同兩點,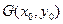 為AB的中點,記A、B兩點連線的斜率為k,證明:
為AB的中點,記A、B兩點連線的斜率為k,證明: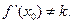
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com