【題目】如圖，已知在四棱錐
中，底面
是邊長為4的正方形，
是正三角形，平面
平面，
分別是
的中點.
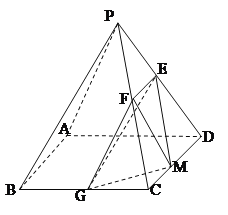
（1）求證：平面
平面
；
（2）若
是線段
上一點，求三棱錐
的體積.
【答案】（1）證明見解析；（2）
.
【解析】
試題分析：（1）要證明面面垂直，只需在一個平面內(nèi)找到另一平面的一條垂線.由已知平面
平面
，且
，可證
平面
，再根據(jù)
是中位線，可證
，從而
平面，進而再證平面
平面，該題實質(zhì)是先找到面的一條垂線
，再將平移到面
內(nèi)；
（2）點
是線段的動點，考慮到和
到面的距離相等，故
，再結合第（1）問結果，取
的中點
連接
，據(jù)面面垂直的性質(zhì)，點到
的距離就是三棱錐
的高，再求
，進而求體積.
試題解析：（1）∵平面平面，平面
平面
，
平面，，
平面，又
中，
分別是
的中點，
，可得平面，
平面，∴平面平面；
（2）
，平面，
平面，
平面，因此上的點
到平面的距離等于點到平面的距離，∴，取的中點連接，則
，
平面，平面，∴
，于是
，
∵平面平面，平面
平面
，
是正三角形，∴點到平面的距離等于正的高，即為
，因此，三棱錐M﹣EFG的體積=
=
.
閱讀快車系列答案科目：高中數(shù)學 來源： 題型：
【題目】為了迎接旅游旺季的到來，少林寺設置了一個專門安排旅客住宿的客棧，寺廟的工作人員發(fā)現(xiàn)為游客準備的食物有些月份剩余不少，浪費很嚴重，為了控制經(jīng)營成本，減少浪費，就想適時調(diào)整投入.為此他們統(tǒng)計每個月入住的游客人數(shù)，發(fā)現(xiàn)每年各個月份來客棧入住的游客人數(shù)會呈現(xiàn)周期性的變化，并且有以下規(guī)律：
①每年相同的月份，入住客棧的游客人數(shù)基本相同；
②入住客棧的游客人數(shù)在
月份最少，在
月份最多，相差約
人；
③月份入住客棧的游客約為
人，隨后逐月增加直到月份達到最多.
（1）試用一個正弦型三角函數(shù)描述一年中入住客棧的游客人數(shù)與月份之間的關系；
（2）請問哪幾個月份要準備份以上的食物？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知一個口袋有
個白球，
個黑球，這些球除顏色外全部相同，現(xiàn)將口袋中的球隨機逐個取出，并依次放入編號為，
，，
的抽屜內(nèi).
（1）求編號為的抽屜內(nèi)放黑球的概率；
（2）口袋中的球放入抽屜后，隨機取出兩個抽屜中的球，求取出的兩個球是一黑一白的概率.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
（1）討論函數(shù)
在定義域上的單調(diào)性；
（2）令函數(shù)
，是自然對數(shù)的底數(shù)，若函數(shù)
有且只有一個零點
，判斷與
的大小，并說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】關于函數(shù)
下列命題錯誤的是( )
A.函數(shù)
的圖像關于
軸對稱
B.在區(qū)間
上，函數(shù)是減函數(shù)
C.函數(shù)的最小值為
D.在區(qū)間
上，函數(shù)是增函數(shù).
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)
，
（1）若f(1)<0，試判斷函數(shù)單調(diào)性并求使不等式
恒成立的
的取值范圍；
（2）若
， 
且
在
上的最小值為-2，求m的值。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，
，（
為自然對數(shù)的底數(shù)），且曲線
與
在坐標原點處的切線相同.
（1）求
的最小值；
（2）若
時，
恒成立，試求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某旅游愛好者計劃從3個亞洲國家A1，A2，A3和3個歐洲國家B1，B2，B3中選擇2個國家去旅游.
(1)若從這6個國家中任選2個，求這2個國家都是亞洲國家的概率；
(2)若從亞洲國家和歐洲國家中各選1個，求這兩個國家包括A1，但不包括B1的概率．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
