
【題目】某學校為了了解全校學生“體能達標”的情況,從全校1000名學生中隨機選出40名學生,參加“體能達標”預測,并且規定“體能達標”預測成績小于60分的為“不合格”,否則為“合格”若該校“不合格”的人數不超過總人數的![]() ,則全校“體能達標”為“合格”;否則該校“體能達標”為“不合格”,需要重新對全校學生加強訓練現將這40名學生隨機分為甲、乙兩個組,其中甲組有24名學生,乙組有16名學生經過預測后,兩組各自將預測成績統計分析如下:甲組的平均成績為70,標準差為4;乙組的平均成績為80,標準差為6(題中所有數據的最后結果都精確到整數).
,則全校“體能達標”為“合格”;否則該校“體能達標”為“不合格”,需要重新對全校學生加強訓練現將這40名學生隨機分為甲、乙兩個組,其中甲組有24名學生,乙組有16名學生經過預測后,兩組各自將預測成績統計分析如下:甲組的平均成績為70,標準差為4;乙組的平均成績為80,標準差為6(題中所有數據的最后結果都精確到整數).
(1)求這40名學生測試成績的平均分![]() 和標準差
和標準差![]() ;
;
(2)假設該校學生的“體能達標”預測服從正態分布![]() 用樣本平均數
用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,用樣本標準差
,用樣本標準差![]() 作為
作為![]() 的估計值
的估計值![]() .利用估計值估計:該校學生“體能達標”預測是否“合格”?
.利用估計值估計:該校學生“體能達標”預測是否“合格”?
附:①![]() 個數
個數![]() 的平均數
的平均數![]() ,方差
,方差![]() ;
;
②若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
【答案】(1)平均分為74,標準差為7.(2)該校學生“體能達標”預測合格.
【解析】
(1)根據甲組的平均成績為70,乙組的平均成績為80,根據公式可得![]()
設甲組24名學生的測試成績分別為:![]() ,乙組16名學生的測試成績分別為:
,乙組16名學生的測試成績分別為:![]() ,將公式
,將公式![]() 變形變形為
變形變形為![]() ,
,
分別求得![]() 和
和![]() ,即可根據公式解得解得
,即可根據公式解得解得![]() 和
和![]() ,最后整理公式得
,最后整理公式得![]() ,計算并求解即可
,計算并求解即可
(2)由(1)可得![]() ,
,![]() ,由
,由![]() ,
,
得![]() ,進而得到
,進而得到![]() ,
,
求出全校學生“不合格”的人數占總人數的百分比,與![]() 進行比較即可
進行比較即可
(1)這40名學生測試成績的平均分![]() .
.
將![]() 變形為
變形為![]() .
.
設第一組學生的測試成績分別為![]() ,
,
第二組學生的測試成績分別為![]() ,則
,則
第一組的方差為
![]() ,
,
解得![]() .
.
第二組的方差為
![]() ,
,
解得![]() .
.
這40名學生的方差為
![]()
![]() ,
,
所以![]() .
.
綜上,這40名學生測試成績的平均分為74,標準差為7.
(2)由![]() ,
,![]() ,得
,得![]() 的估計值為
的估計值為![]() ,
,![]() 的估計值
的估計值![]() .
.
由![]() ,得
,得![]() ,
,
即![]() .所以
.所以
![]() ,
,
從而,在全校1000名學生中,“不合格”的有![]() (人),
(人),
而![]() ,
,
故該校學生“體能達標”預測合格.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在某項娛樂活動的海選過程中評分人員需對同批次的選手進行考核并評分,并將其得分作為該選手的成績,成績大于等于60分的選手定為合格選手,直接參加第二輪比賽,不超過40分的選手將直接被淘汰,成績在![]() 內的選手可以參加復活賽,如果通過,也可以參加第二輪比賽.
內的選手可以參加復活賽,如果通過,也可以參加第二輪比賽.
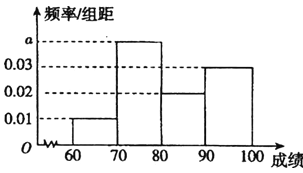
(1)已知成績合格的200名參賽選手成績的頻率分布直方圖如圖,求a的值及估計這200名參賽選手的成績平均數;
(2)根據已有的經驗,參加復活賽的選手能夠進入第二輪比賽的概率為![]() ,假設每名選手能否通過復活賽相互獨立,現有3名選手進入復活賽,記這3名選手在復活賽中通過的人數為隨機變量X,求X的分布列和數學期望.
,假設每名選手能否通過復活賽相互獨立,現有3名選手進入復活賽,記這3名選手在復活賽中通過的人數為隨機變量X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
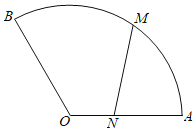
【題目】某公園草坪上有一扇形小徑(如圖),扇形半徑為![]() ,中心角為
,中心角為![]() ,甲由扇形中心
,甲由扇形中心![]() 出發沿
出發沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同時乙從
快走,同時乙從![]() 出發,沿扇形弧以每秒
出發,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,記
慢跑,記![]() 秒時甲、乙兩人所在位置分別為
秒時甲、乙兩人所在位置分別為![]() ,
,![]() ,通過計算
,通過計算![]() ,判斷下列說法是否正確:
,判斷下列說法是否正確:
(1)當![]() 時,函數
時,函數![]() 取最小值;
取最小值;
(2)函數![]() 在區間
在區間![]() 上是增函數;
上是增函數;
(3)若![]() 最小,則
最小,則![]() ;
;
(4)![]() 在
在![]() 上至少有兩個零點;
上至少有兩個零點;
其中正確的判斷序號是______(把你認為正確的判斷序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求證:數列{an-1}是等比數列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果對任意n∈N*,都有bn+![]() t≤t2,求實數t的取值范圍.
t≤t2,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的長軸長為
的長軸長為![]() ,點
,點![]() 、
、![]() 、
、![]() 為橢圓上的三個點,
為橢圓上的三個點,![]() 為橢圓的右端點,
為橢圓的右端點,![]() 過中心
過中心![]() ,且
,且![]() ,
,![]() .
.

(1)求橢圓的標準方程;
(2)設![]() 、
、![]() 是橢圓上位于直線
是橢圓上位于直線![]() 同側的兩個動點(異于
同側的兩個動點(異于![]() 、
、![]() ),且滿足
),且滿足![]() ,試討論直線
,試討論直線![]() 與直線
與直線![]() 斜率之間的關系,并求證直線
斜率之間的關系,并求證直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有人玩擲均勻硬幣走跳棋的游戲,棋盤上標有第0站(出發地),第1站,第2站,……,第100站. 一枚棋子開始在出發地,棋手每擲一次硬幣,這枚棋子向前跳動一次,若擲出正向,棋子向前跳一站,若擲出反面,棋子向前跳兩站,直到棋子跳到第99站(獲勝)或跳到第100站(失敗)時,該游戲結束. 設棋子跳到第![]() 站的概率為
站的概率為![]() .
.
(1)求![]() ,
,![]() ,
,![]() ,并根據棋子跳到第
,并根據棋子跳到第![]() 站的情況寫出
站的情況寫出![]() 與
與![]() 、
、![]() 的遞推關系式(
的遞推關系式(![]() );
);
(2)求證:數列![]()
![]() 為等比數列;
為等比數列;
(3)求玩該游戲獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 是橢圓
是橢圓![]() 的左、右頂點,
的左、右頂點,![]() 為橢圓上異于
為橢圓上異于![]() 、
、![]() 的一點.
的一點.
(1)![]() 是橢圓
是橢圓![]() 的上頂點,且直線
的上頂點,且直線![]() 與直線
與直線![]() 垂直,求點
垂直,求點![]() 到
到![]() 軸的距離;
軸的距離;
(2)過點![]() 的直線
的直線![]() (不過坐標原點)與橢圓
(不過坐標原點)與橢圓![]() 交于
交于![]() 、
、![]() 兩點,且點
兩點,且點![]() 在
在![]() 軸上方,點
軸上方,點![]() 在
在![]() 軸下方,若
軸下方,若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解全市統考情況,從所有參加考試的考生中抽取4000名考生的成績,頻率分布直方圖如下圖所示.

(1)求這4000名考生的半均成績![]() (同一組中數據用該組區間中點作代表);
(同一組中數據用該組區間中點作代表);
(2)由直方圖可認為考生考試成績z服從正態分布![]() ,其中
,其中![]() 分別取考生的平均成績
分別取考生的平均成績![]() 和考生成績的方差
和考生成績的方差![]() ,那么抽取的4000名考生成績超過84.81分(含84.81分)的人數估計有多少人?
,那么抽取的4000名考生成績超過84.81分(含84.81分)的人數估計有多少人?
(3)如果用抽取的考生成績的情況來估計全市考生的成績情況,現從全市考生中隨機抽取4名考生,記成績不超過84.81分的考生人數為![]() ,求
,求![]() .(精確到0.001)
.(精確到0.001)
附:①![]() ;
;
②![]() ,則
,則![]() ;
;
③![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com