
【題目】已知函數![]() ,
,![]() .
.
(1)求函數![]() 的極大值.
的極大值.
(2)當![]() 時,證明函數
時,證明函數![]() 有且只有一個零點.
有且只有一個零點.
【答案】(1) 當![]() 或
或![]() 時,
時, ![]() 無極大值;
無極大值;
當![]() 時
時![]() 的極大值為
的極大值為![]() .
.
當![]() 時
時![]() 的極大值為
的極大值為![]()
【解析】
(1)求導得![]() ,再討論
,再討論![]() 與1的關系判定即可.
與1的關系判定即可.
(2)根據函數的單調性以及極大值![]() ,結合單調性即可轉證
,結合單調性即可轉證![]() ,
,![]() 有解.參變分離可得
有解.參變分離可得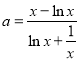 ,再分析
,再分析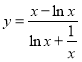 的單調性求出值域即可判定
的單調性求出值域即可判定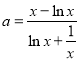 有唯一解即可.
有唯一解即可.
(1) ![]() .令
.令![]() 可得
可得![]() .
.
①當![]() 時,易得
時,易得![]() ,故當
,故當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
故![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,此時
上單調遞增,此時![]() 無極大值.
無極大值.
②當![]() 時, 當
時, 當![]() 時,
時, ![]() ;當
;當![]() 時,
時,![]() 與
與![]() .
.
故![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() ,
,![]() 上單調遞增.故函數
上單調遞增.故函數![]() 的極大值為
的極大值為![]() .
.
③當![]() 時,
時, ![]() 恒成立. 此時
恒成立. 此時![]() 無極大值.
無極大值.
④當![]() 時, 當
時, 當![]() 時,
時, ![]() ;當
;當![]() 時,
時,![]() 與
與![]() .
.
故![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() ,
,![]() 上單調遞增.故函數
上單調遞增.故函數![]() 的極大值為
的極大值為![]() .
.
綜上所述, 當![]() 或
或![]() 時,
時, ![]() 無極大值;
無極大值;
當![]() 時
時![]() 的極大值為
的極大值為![]() .
.
當![]() 時
時![]() 的極大值為
的極大值為![]()
(2)由(1),當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() ,
,![]() 上單調遞增.
上單調遞增.
且極大值為![]() .故當
.故當![]() 時,
時,![]() .故
.故![]() 在
在![]() 無零點.
無零點.
又因為![]() 在
在![]() 上單調遞增,故要證明函數
上單調遞增,故要證明函數![]() 有且只有一個零點,即證明
有且只有一個零點,即證明![]() ,
,![]() 有解即可.
有解即可.
參變分離有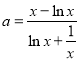 ,令
,令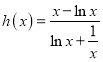 ,
,
則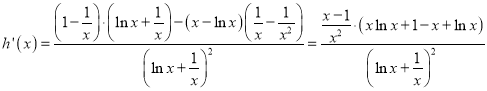 .
.
因為![]() ,故考慮
,故考慮![]() 的正負.
的正負.
又![]() ,
,![]() .
.
故![]() 為增函數.
為增函數.
又![]() ,故
,故![]() ,即
,即![]() .
.
故![]() ,故
,故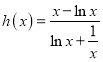 為增函數.故
為增函數.故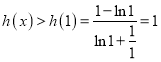 .
.
故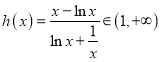 .故當
.故當![]() 時
時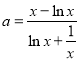 恒有解.
恒有解.
即![]() 有且僅有一根.得證.
有且僅有一根.得證.


科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 分別是
分別是![]() 的邊
的邊![]() ,
,![]() 上的一點,
上的一點,![]() ,將
,將![]() 沿
沿![]() 折起為
折起為![]() ,使
,使![]() 點位于
點位于![]() 點的位置,連接
點的位置,連接![]() ,
,![]() ,
,![]() .
.
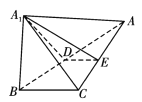
(1)若![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,平面
的中點,平面![]() 與平面
與平面![]() 的交線為
的交線為![]() ,證明:
,證明:![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() 與
與![]() 的面積分別為4和9,
的面積分別為4和9,![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年底,北京2022年冬奧組委會啟動志愿者全球招募,僅一個月內報名人數便突破60萬,其中青年學生約有50萬人.現從這50萬青年學生志愿者中,按男女分層抽樣隨機選取20人進行英語水平測試,所得成績(單位:分)統計結果用莖葉圖記錄如下:

(Ⅰ)試估計在這50萬青年學生志愿者中,英語測試成績在80分以上的女生人數;
(Ⅱ)從選出的8名男生中隨機抽取2人,記其中測試成績在70分以上的人數為X,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)為便于聯絡,現將所有的青年學生志愿者隨機分成若干組(每組人數不少于5000),并在每組中隨機選取![]() 個人作為聯絡員,要求每組的聯絡員中至少有1人的英語測試成績在70分以上的概率大于90%.根據圖表中數據,以頻率作為概率,給出
個人作為聯絡員,要求每組的聯絡員中至少有1人的英語測試成績在70分以上的概率大于90%.根據圖表中數據,以頻率作為概率,給出![]() 的最小值.(結論不要求證明)
的最小值.(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】超級病菌是一種耐藥性細菌,產生超級細菌的主要原因是用于抵抗細菌侵蝕的藥物越來越多,但是由于濫用抗生素的現象不斷的發生,很多致病菌也對相應的抗生素產生了耐藥性,更可怕的是,抗生素藥物對它起不到什么作用,病人會因為感染而引起可怕的炎癥,高燒、痙攣、昏迷直到最后死亡.某藥物研究所為篩查某種超級細菌,需要檢驗血液是否為陽性,現有n(![]() )份血液樣本,每個樣本取到的可能性均等,有以下兩種檢驗方式:
)份血液樣本,每個樣本取到的可能性均等,有以下兩種檢驗方式:
(1)逐份檢驗,則需要檢驗n次;
(2)混合檢驗,將其中k(![]() 且
且![]() )份血液樣本分別取樣混合在一起檢驗,若檢驗結果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數總共為
)份血液樣本分別取樣混合在一起檢驗,若檢驗結果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數總共為![]() 次,假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為p(
次,假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為p(![]() ).
).
(1)假設有5份血液樣本,其中只有2份樣本為陽性,若采用逐份檢驗方式,求恰好經過2次檢驗就能把陽性樣本全部檢驗出來的概率;
(2)現取其中k(![]() 且
且![]() )份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為
)份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為![]() ,采用混合檢驗方式,樣本需要檢驗的總次數為
,采用混合檢驗方式,樣本需要檢驗的總次數為![]() .
.
(i)試運用概率統計的知識,若![]() ,試求p關于k的函數關系式
,試求p關于k的函數關系式![]() ;
;
(ii)若![]() ,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數期望值更少,求k的最大值.
,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數期望值更少,求k的最大值.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記![]() 表示m,n中的最大值,如
表示m,n中的最大值,如![]() .已知函數
.已知函數![]() ,
,![]() .
.
(1)設![]() ,求函數
,求函數![]() 在
在![]() 上的零點個數;
上的零點個數;
(2)試探討是否存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立?若存在,求a的取值范圍;若不存在,說明理由.
恒成立?若存在,求a的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=aex,g(x)=lnx-lna,其中a為常數,且曲線y=f(x)在其與y軸的交點處的切線記為l1,曲線y=g(x)在其與x軸的交點處的切線記為l2,且l1∥l2.
(1)求l1,l2之間的距離;
(2)若存在x使不等式![]() 成立,求實數m的取值范圍;
成立,求實數m的取值范圍;
(3)對于函數f(x)和g(x)的公共定義域中的任意實數x0,稱|f(x0)-g(x0)|的值為兩函數在x0處的偏差.求證:函數f(x)和g(x)在其公共定義域內的所有偏差都大于2.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com