
【題目】過橢圓![]() 的右焦點F作直線
的右焦點F作直線![]() 交橢圓于M、N兩點,H為線段MN的中點,且OH的斜率為
交橢圓于M、N兩點,H為線段MN的中點,且OH的斜率為![]() ,設點
,設點![]()
![]() 求該橢圓的方程;
求該橢圓的方程;
![]() 若點P是橢圓上的動點,求線段PA的中點G的軌跡方程;
若點P是橢圓上的動點,求線段PA的中點G的軌跡方程;
![]() 過原點的直線交橢圓于B、C兩點,求
過原點的直線交橢圓于B、C兩點,求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() ;(2)
;(2) ,(3)最大值
,(3)最大值![]() .
.
【解析】
![]() 結合點差法和直線的斜率,以及OH的斜率為
結合點差法和直線的斜率,以及OH的斜率為![]() ,可得
,可得![]() ,再根據右焦點F在直線
,再根據右焦點F在直線![]() 上,求出c,即可求出橢圓的方程;
上,求出c,即可求出橢圓的方程;
![]() 利用轉移法解得G的軌跡方程;
利用轉移法解得G的軌跡方程;
![]() 聯立直線的方程與橢圓方程,利用弦長公式求出CB,再根據點到直線距離公式得A到CB的距離,根據三角形的面積得函數解析式,根據基本不等式求出最大值.
聯立直線的方程與橢圓方程,利用弦長公式求出CB,再根據點到直線距離公式得A到CB的距離,根據三角形的面積得函數解析式,根據基本不等式求出最大值.
解:![]() 設
設![]() ,
,![]() 則
則 ,兩式相減可得,
,兩式相減可得,
![]() ,
,
即![]() ,
,
![]()
![]() 直線
直線![]() 交橢圓于M、N兩點,H為線段MN的中點,且OH的斜率為
交橢圓于M、N兩點,H為線段MN的中點,且OH的斜率為![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
![]() 右焦點F作在直線
右焦點F作在直線![]() 上,
上,
令![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() ,
,![]() ,
,
![]() 橢圓方程為
橢圓方程為![]() ;
;
![]() 設
設![]() ,
,![]() ,則有
,則有 ,即
,即 ,代入為
,代入為![]() 中,
中,
得![]() ,
,
故線段PA的中點G的軌跡方程為 ,
,
![]() 當直線BC垂直x軸時,此時
當直線BC垂直x軸時,此時![]() ,點A到直線BC的距離
,點A到直線BC的距離![]() ,則
,則![]() ,
,
當直線BC的斜率為零時,此時![]() ,點A到直線BC的距離
,點A到直線BC的距離![]() ,則
,則![]() ,
,
當直線BC的斜率存在且不為零時,設直線BC的方程為![]() ,
,
聯立方程組可得 ,消y整理可得
,消y整理可得![]() ,
,
解得![]() ,
,![]() ,
,
則![]() ,
,
點A到直線BC的距離![]() ,
,
![]()
![]() ,
,
![]() ,
,
當且僅當![]() 時,即
時,即![]() ,
,![]() 取最大值,最大值為
取最大值,最大值為![]() ,
,
綜上所述![]() 面積的最大值
面積的最大值![]() .
.


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:
【題目】在以下命題中,不正確的個數為( )
①![]() 是
是![]() ,b共線的充要條件;②若
,b共線的充要條件;②若![]() ∥
∥![]() ,則存在唯一的實數λ,使
,則存在唯一的實數λ,使![]() =λ
=λ![]() ;③對空間任意一點O和不共線的三點A,B,C,若
;③對空間任意一點O和不共線的三點A,B,C,若![]() =2
=2![]() -2
-2![]() -
-![]() ,則P,A,B,C四點共面;④若{
,則P,A,B,C四點共面;④若{![]() ,
,![]() ,
,![]() }為空間的一個基底,則{
}為空間的一個基底,則{![]() +
+![]() ,
,![]() +
+![]() ,
,![]() +
+![]() }構成空間的另一個基底;⑤ |(
}構成空間的另一個基底;⑤ |(![]() ·
·![]() )·
)·![]() |=|
|=|![]() |·|
|·|![]() |·|
|·|![]() |.
|.
A. 2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,橢圓
兩點,橢圓![]() 的右頂點為
的右頂點為![]() ,且滿足
,且滿足![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 、
、![]() ,且定點
,且定點![]() 滿足
滿足![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明在石家莊市某物流派送公司找到了一份派送員的工作,該公司給出了兩種日薪薪酬方案.甲方案:底薪100元,每派送一單獎勵1元;乙方案:底薪140元,每日前55單沒有獎勵,超過55單的部分每單獎勵12元.
(1)請分別求出甲、乙兩種薪酬方案中日薪![]() (單位:元)與送貨單數
(單位:元)與送貨單數![]() 的函數關系式;
的函數關系式;
(2)根據該公司所有派送員100天的派送記錄,發現派送員的日平均派送單數與天數滿足以下表格:
日均派送單數 | 52 | 54 | 56 | 58 | 60 |
頻數(天) | 20 | 30 | 20 | 20 | 10 |
回答下列問題:
①根據以上數據,設每名派送員的日薪為![]() (單位:元),試分別求出這100天中甲、乙兩種方案的日薪
(單位:元),試分別求出這100天中甲、乙兩種方案的日薪![]() 平均數及方差;
平均數及方差;
②結合①中的數據,根據統計學的思想,幫助小明分析,他選擇哪種薪酬方案比較合適,并說明你的理由.
(參考數據: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
【答案】(1) ;(2)見解析
;(2)見解析
【解析】試題分析:(1)甲方案:底薪100元,每派送一單獎勵1元;乙方案:底薪140元,每日前55單沒有獎勵,超過55單的部分每單獎勵12元. 求出甲、乙兩種薪酬方案中日薪![]() (單位:元)與送貨單數
(單位:元)與送貨單數![]() 的函數關系式;
的函數關系式;
①、由表格可知,甲方案中,日薪為152元的有20天,日薪為154元的有30天,日薪為156元的有20天,日薪為158元的有20天,日薪為160元的有10天,由此可求出這100天中甲方案的日薪![]() 平均數及方差:同理可求出這100天中乙兩種方案的日薪
平均數及方差:同理可求出這100天中乙兩種方案的日薪![]() 平均數及方差,
平均數及方差,
②不同的角度可以有不同的答案
試題解析:((1)甲方案中派送員日薪![]() (單位:元)與送貨單數
(單位:元)與送貨單數![]() 的函數關系式為:
的函數關系式為: ![]() ,
,
乙方案中派送員日薪![]() (單位:元)與送單數
(單位:元)與送單數![]() 的函數關系式為:
的函數關系式為:
![]() ,
,
(2)①、由表格可知,甲方案中,日薪為152元的有20天,日薪為154元的有30天,日薪為156元的有20天,日薪為158元的有20天,日薪為160元的有10天,則
![]()
![]() ,
,
 ,
,
乙方案中,日薪為140元的有50天,日薪為152元的有20天,日薪為176元的有20天,日薪為200元的有10天,則
![]()
![]() ,
,
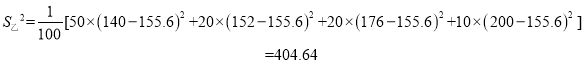
②、答案一:
由以上的計算可知,雖然![]() ,但兩者相差不大,且
,但兩者相差不大,且![]() 遠小于
遠小于![]() ,即甲方案日薪收入波動相對較小,所以小明應選擇甲方案.
,即甲方案日薪收入波動相對較小,所以小明應選擇甲方案.
答案二:
由以上的計算結果可以看出, ![]() ,即甲方案日薪平均數小于乙方案日薪平均數,所以小明應選擇乙方案.
,即甲方案日薪平均數小于乙方案日薪平均數,所以小明應選擇乙方案.
【題型】解答題
【結束】
20
【題目】已知橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
, ![]() ,且離心率為
,且離心率為![]() ,
, ![]() 為橢圓上任意一點,當
為橢圓上任意一點,當![]() 時,
時, ![]() 的面積為1.
的面積為1.
(1)求橢圓![]() 的方程;
的方程;
(2)已知點![]() 是橢圓
是橢圓![]() 上異于橢圓頂點的一點,延長直線
上異于橢圓頂點的一點,延長直線![]() ,
, ![]() 分別與橢圓交于點
分別與橢圓交于點![]() ,
, ![]() ,設直線
,設直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求證:
,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汕尾市基礎教育處為調查在校中學生每天放學后的自學時間情況,在本市的所有中學生中隨機抽取了120名學生進行調查,現將日均自學時間小于1小時的學生稱為“自學不足”者![]() 根據調查結果統計后,得到如下
根據調查結果統計后,得到如下![]() 列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為
列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為![]() .
.
非自學不足 | 自學不足 | 合計 | |
配有智能手機 | 30 | ||
沒有智能手機 | 10 | ||
合計 |
![]() 請完成上面的列聯表;
請完成上面的列聯表;
![]() 根據列聯表的數據,能否有
根據列聯表的數據,能否有![]() 的把握認為“自學不足”與“配有智能手機”有關?
的把握認為“自學不足”與“配有智能手機”有關?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的部分圖象大致是( )
的部分圖象大致是( )
A.  B.
B. 
C.  D.
D. 
【答案】D
【解析】當![]() 時,
時, ![]() ,所以去掉A,B;
,所以去掉A,B;
因為![]() ,所以
,所以![]() ,因此去掉C,選D.
,因此去掉C,選D.
點睛:有關函數圖象識別問題的常見題型及解題思路(1)由解析式確定函數圖象的判斷技巧:(1)由函數的定義域,判斷圖象左右的位置,由函數的值域,判斷圖象的上下位置;②由函數的單調性,判斷圖象的變化趨勢;③由函數的奇偶性,判斷圖象的對稱性;④由函數的周期性,判斷圖象的循環往復.(2)由實際情景探究函數圖象.關鍵是將問題轉化為熟悉的數學問題求解,要注意實際問題中的定義域問題.
【題型】單選題
【結束】
8
【題目】《九章算術》中,將底面是直角三角形的直三棱柱稱之為“塹堵”,已知某“塹堵”的三視圖如圖所示,則該“塹堵”的外接球的表面積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 三個內角
三個內角![]() 所對的邊分別是
所對的邊分別是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圓半徑為2,求
的外接圓半徑為2,求![]() 周長的最大值.
周長的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)由正弦定理將邊角關系化為邊的關系![]() ,再根據余弦定理求角
,再根據余弦定理求角![]() ,(2)先根據正弦定理求邊,用角表示周長,根據兩角和正弦公式以及配角公式化為基本三角函數,最后根據正弦函數性質求最大值.
,(2)先根據正弦定理求邊,用角表示周長,根據兩角和正弦公式以及配角公式化為基本三角函數,最后根據正弦函數性質求最大值.
試題解析:(1)由正弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
因為![]() ,則
,則![]() .
.
(2)由正弦定理![]()
∴![]() ,
, ![]() ,
, ![]() ,
,
∴周長![]()
![]()
![]()
![]()
![]()
![]()
∵![]() ,∴
,∴![]()
∴當![]() 即
即![]() 時
時![]()
∴當![]() 時,
時, ![]() 周長的最大值為
周長的最大值為![]() .
.
【題型】解答題
【結束】
18
【題目】經調查,3個成年人中就有一個高血壓,那么什么是高血壓?血壓多少是正常的?經國際衛生組織對大量不同年齡的人群進行血壓調查,得出隨年齡變化,收縮壓的正常值變化情況如下表:

其中:  ,
, ![]() ,
, ![]()

(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;(
;(![]() 的值精確到0.01)
的值精確到0.01)
(3)若規定,一個人的收縮壓為標準值的0.9~1.06倍,則為血壓正常人群;收縮壓為標準值的1.06~1.12倍,則為輕度高血壓人群;收縮壓為標準值的1.12~1.20倍,則為中度高血壓人群;收縮壓為標準值的1.20倍及以上,則為高度高血壓人群.一位收縮壓為180mmHg的70歲的老人,屬于哪類人群?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 是
是![]() 所在平面內一點,下列說法正確的是( )
所在平面內一點,下列說法正確的是( )
A.若![]() ,則
,則![]() 的形狀為等邊三角形
的形狀為等邊三角形
B.若![]() ,則點
,則點![]() 是邊
是邊![]() 的中點
的中點
C.過![]() 任作一條直線,再分別過頂點
任作一條直線,再分別過頂點![]() 作
作![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,若
,若![]() 恒成立,則點
恒成立,則點![]() 是
是![]() 的垂心
的垂心
D.若![]() 則點
則點![]() 在邊
在邊![]() 的延長線上
的延長線上
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com