
【題目】已知函數![]() .
.
(Ⅰ)若函數![]() 在
在![]() 處取得極值,求實數
處取得極值,求實數![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,函數![]() (其中
(其中![]() 為函數
為函數![]() 的導數)的圖像關于直線
的導數)的圖像關于直線![]() 對稱,求函數
對稱,求函數![]() 單調區間;
單調區間;
(Ⅲ)在(Ⅱ)的條件下,若對任意的![]() ,都有
,都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)函數
;(Ⅱ)函數![]() 在區間
在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減;(Ⅲ)
上單調遞減;(Ⅲ) ![]() .
.
【解析】
試題分析:(Ⅰ)由![]() ,得
,得![]() ;(Ⅱ)
;(Ⅱ)![]() 的圖象關于直線
的圖象關于直線![]() 對稱,故函數
對稱,故函數![]() 為偶函數,解得
為偶函數,解得![]() ,分別令
,分別令![]() ,
,![]() 即可得到單調區間;(Ⅲ)對任意的
即可得到單調區間;(Ⅲ)對任意的![]() ,都有
,都有![]() 恒成立可轉化為
恒成立可轉化為![]() 在
在![]() 上恒成立,易知
上恒成立,易知![]() ,∴
,∴![]() 在
在![]() 上恒成立,構造函數
上恒成立,構造函數![]() ,只需
,只需![]() 即可.
即可.
試題解析:(Ⅰ)由![]() 有
有![]()
因為![]() 在
在![]() 處取得極值,故
處取得極值,故![]()
∴![]()
經檢驗:當![]() 時,符合題意,故
時,符合題意,故![]() .
.
(Ⅱ)由(Ⅰ)知:![]()
∵![]() 的圖像關于直線
的圖像關于直線![]() 對稱,故函數
對稱,故函數![]() 為偶函數
為偶函數
又![]()
![]()
∴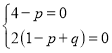 ,解得
,解得![]()
∴![]()
∴![]()
令![]() 有
有![]() 或
或![]()
令![]() 有
有![]() 或
或![]()
∴函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
在區間![]() 上單調遞減.
上單調遞減.
(Ⅲ)由(Ⅱ)知,對任意的![]() ,都有
,都有![]() 恒成立可轉化為
恒成立可轉化為
![]() 在
在![]() 上恒成立
上恒成立
易知![]() ∴
∴![]() 在
在![]() 上恒成立
上恒成立
令![]() ,∴
,∴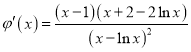
令![]() ,∴
,∴![]()
∴![]() 在
在![]() 上遞減,
上遞減,![]() 上遞增
上遞增
∴![]()
∴![]() ,即
,即![]() 在
在![]() 上遞增
上遞增
∴![]()
∴![]() .
.


科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,上頂點為
,上頂點為![]() ,過
,過![]() 與
與![]() 垂直的直線交
垂直的直線交![]() 軸負半軸于
軸負半軸于![]() 點,且
點,且![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)若過![]() 、
、![]() 、
、![]() 三點的圓恰好與直線
三點的圓恰好與直線![]() 相切,求橢圓
相切,求橢圓![]() 的方程;
的方程;
(3)過![]() 的直線
的直線![]() 與(2)中橢圓交于不同的兩點
與(2)中橢圓交于不同的兩點![]() 、
、![]() ,則
,則![]() 的內切圓的面積是否存在最大值?若存在,求出這個最大值及此時的直線方程;若不存在,請說明理由.
的內切圓的面積是否存在最大值?若存在,求出這個最大值及此時的直線方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A. 在殘差圖中,殘差點分布的帶狀區域的寬度越狹窄,其模型擬合的精度越高
B. 在線性回歸分析中,回歸直線不一定過樣本點的中心![]()
C. 在回歸分析中, ![]() 為0.98的模型比
為0.98的模型比![]() 為0.80的模型擬合的效果好
為0.80的模型擬合的效果好
D. 自變量取值一定時,因變量的取值帶有一定隨機性的兩個變量之間的關系叫做相關關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一項針對人們休閑方式的調查結果如下:受調查對象總計124人,其中女性70人,男性54人.女性中有43人主要的休閑方式是看電視,另外27人主要的休閑方式是運動;男性中有21人主要的休閑方式是看電視,另外33人主要的休閑方式是運動.
(1)根據以上數據建立一個![]() 的列聯表;
的列聯表;
(2)根據下列提供的獨立檢驗臨界值表,你最多能有多少把握認為性別與休閑方式有關系?
獨立檢驗臨界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
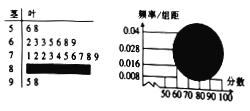
【題目】如圖,某校高一(1)班全體男生的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分,據此解答如下問題:
(1)求該班全體男生的人數及分數在![]() 之間的男生人數;
之間的男生人數;
(2)根據頻率分布直方圖,估計該班全體男生的數學平均成績(同一組中的數據用該組區間的中點值代表);
(3)從分數在![]() 中抽取兩個男生,求抽取的兩男生分別來自
中抽取兩個男生,求抽取的兩男生分別來自![]() 、
、![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
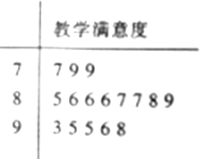
【題目】某學校用“10分制”調查本校學生對教師教學的滿意度,現從學生中隨機抽取16名,以下莖葉圖記錄了他們對該校教師教學滿意度的分數(以小數點前的一位數字為莖,小數點后的一位數字為葉):
(Ⅰ)若教學滿意度不低于9.5分,則稱該生對教師的教學滿意度為“極滿意”.求從這16人中隨機選取3人,至少有1人是“極滿意”的概率;
(Ⅱ)以這16人的樣本數據來估計整個學校的總體數據,若從該校所有學生中(學生人數很多)任選3人,記![]() 表示抽到“極滿意”的人數,求
表示抽到“極滿意”的人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經測算,某型號汽車在勻速行駛過程中每小時耗油量![]() (升)與速度
(升)與速度![]() (千米/每小時)
(千米/每小時) ![]() 的關系可近似表示為:
的關系可近似表示為: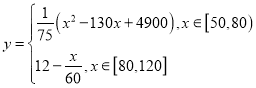 .
.
(Ⅰ)該型號汽車速度為多少時,可使得每小時耗油量最低?
(Ⅱ)已知![]() 兩地相距120公里,假定該型號汽車勻速從
兩地相距120公里,假定該型號汽車勻速從![]() 地駛向
地駛向![]() 地,則汽車速度為多少時總耗油量最少?
地,則汽車速度為多少時總耗油量最少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知焦點在![]() 軸上的橢圓
軸上的橢圓![]() 的中心是原點
的中心是原點![]() ,離心率為
,離心率為![]() ,以橢圓
,以橢圓![]() 的端州的兩端點和兩焦點所圍成的四邊形的周長為8,直線
的端州的兩端點和兩焦點所圍成的四邊形的周長為8,直線![]() :
:![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于不同兩點
交于不同兩點![]() ,
,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的方程
的方程![]() 為拋物線
為拋物線![]() 上一點,
上一點,![]() 為拋物線的焦點.
為拋物線的焦點.
(I)求![]() ;
;
(II)設直線![]() 與拋物線
與拋物線![]() 有唯一公共點
有唯一公共點![]() ,且與直線
,且與直線![]() 相交于點
相交于點![]() ,試問,在坐標平面內是否存在點
,試問,在坐標平面內是否存在點![]() ,使得以
,使得以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com