【題目】如圖,在四棱錐
中,
,底面ABCD是邊長為3的正方形,EFG分別是棱ABPBPC的中點,
,
.
(Ⅰ)求證:平面EFG∥平面PAD;
(Ⅱ)求三棱錐
的體積.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為F，點
在此拋物線上，
，不過原點的直線
與拋物線C交于A，B兩點，以AB為直徑的圓M過坐標原點．
(1)求拋物線C的方程；
(2)證明：直線恒過定點；
(3)若線段AB中點的縱坐標為2，求此時直線和圓M的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業生產一種產品，從流水線上隨機抽取100件產品，統計其質量指標值并繪制頻率分布直方圖（如圖）：
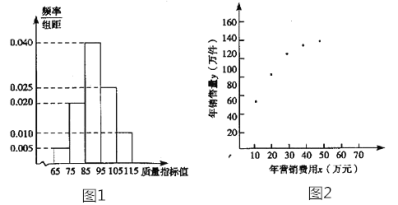
規定產品的質量指標值在
的為劣質品，在
的為優等品，在
的為特優品，銷售時劣質品每件虧損1元，優等品每件盈利3元，特優品每件盈利5元.以這100 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
（1）求每件產品的平均銷售利潤；
（2）該企業為了解年營銷費用
（單位：萬元）對年銷售量
（單位：萬件）的影響，對近5年年營銷費用
和年銷售量
數據做了初步處理，得到如圖的散點圖及一些統計量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中
，
，
，
.
根據散點圖判斷，
可以作為年銷售量（萬件）關于年營銷費用（萬元）的回歸方程.
①求關于的回歸方程；
⑦用所求的回歸方程估計該企業應投人多少年營銷費，才能使得該企業的年收益的預報值達到最大？（收益=銷售利潤營銷費用，取
）
附：對于一組數據
，
，…，
其回歸直線
均斜率和截距的最小二乘估計分別為
，
.
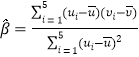查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某籃球運動員的投籃命中率為
，他想提高自己的投籃水平，制定了一個夏季訓練計劃
為了了解訓練效果，執行訓練前，他統計了10場比賽的得分，計算出得分的中位數為15分，平均得分為15分，得分的方差為
執行訓練后也統計了10場比賽的得分，成績莖葉圖如圖所示：
請計算該籃球運動員執行訓練后統計的10場比賽得分的中位數、平均得分與方差；
如果僅從執行訓練前后統計的各10場比賽得分數據分析，你認為訓練計劃對該運動員的投籃水平的提高是否有幫助？為什么？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著中國教育改革的不斷深入，越來越多的教育問題不斷涌現.“衡水中學模式”入駐浙江，可以說是應試教育與素質教育的強烈碰撞.這一事件引起了廣大市民的密切關注.為了了解廣大市民關注教育問題與性別是否有關，記者在北京，上海，深圳隨機調查了100位市民，其中男性55位，女性45位.男性中有45位關注教育問題，其余的不關注教育問題；女性中有30位關注教育問題，其余的不關注教育問題.
（1）根據以上數據完成下列2×2列聯表；
關注教育問題 | 不關注教育問題 | 合計 | |||||
女 | 30 | 45 | |||||
男 | 45 | 55 | |||||
合計 |
| 100 | |||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | ||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | ||
（2）能否在犯錯誤的概率不超過0.025的前提下認為是否關注教育與性別有關系？
參考公式：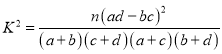
，其中
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知2017年
市居民平均家庭凈收入走勢圖（家庭凈收入=家庭總收入一家庭總支出），如圖所示，則下列說法錯誤的是（ ）
A. 2017年2月份市居國民的平均家庭凈收入最低
B. 2017年4，5，6月份市居民的平均家庭凈收入比7、8、9月份的平均家庭凈收入波動小
C. 2017年有3個月市居民的平均家庭凈收入低于4000元
D. 2017年9、10、11、12月份平均家庭凈收入持續降低
查看答案和解析>>
科目：高中數學 來源： 題型：
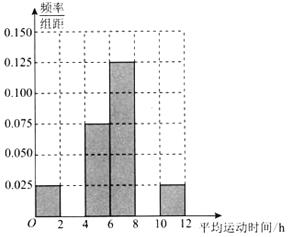
【題目】已知某企業有職工5000人，其中男職工3500人，女職工1500人．該企業為了豐富職工的業余生活，決定新建職工活動中心，為此，該企業工會采用分層抽樣的方法，隨機抽取了300名職工每周的平均運動時間（單位：h），匯總得到頻率分布表（如表所示），并據此來估計該企業職工每周的運動時間：
平均運動時間 | 頻數 | 頻率 |
[0，2） | 15 | 0.05 |
[2，4） | m | 0.2 |
[4，6） | 45 | 0.15 |
[6，8） | 755 | 0.25 |
[8，10） | 90 | 0.3 |
[10，12） | p | n |
合計 | 300 | 1 |
（1）求抽取的女職工的人數；
（2）①根據頻率分布表，求出m、n、p的值，完成如圖所示的頻率分布直方圖，并估計該企業職工每周的平均運動時間不低于4h的概率；
男職工 | 女職工 | 總計 | |
平均運動時間低于4h | |||
平均運動時間不低于4h | |||
總計 |
②若在樣本數據中，有60名女職工每周的平均運動時間不低于4h，請完成以下2×2列聯表，并判斷是否有95%以上的把握認為“該企業職工毎周的平均運動時間不低于4h與性別有關”．
附：K2=
，其中n=a+b+c+d．
P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平行四邊形
中，
，
，過
點作
的垂線，交的延長線于點
，
.連結
，交
于點
，如圖1，將
沿折起，使得點到達點
的位置，如圖2.
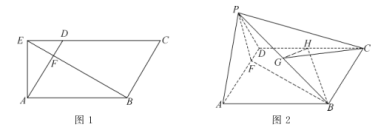
（1）證明：平面
平面
；
（2）若
為
的中點，
為的中點，且平面
平面，求三棱錐
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
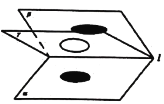
【題目】如圖，
，
，
是由直線
引出的三個不重合的半平面，其中二面角
大小為60°，在二面角內繞直線旋轉，圓
在內，且圓在，內的射影分別為橢圓
，
.記橢圓，的離心率分別為
，
，則
的取值范圍是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
