
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面ABCD,底面ABCD為梯形,
底面ABCD,底面ABCD為梯形,![]() ,
,![]() ,且
,且![]() .
.

(1)在PD上是否存在一點(diǎn)F,使得![]() 平面PAB,若存在,找出F的位置,若不存在,請(qǐng)說(shuō)明理由;
平面PAB,若存在,找出F的位置,若不存在,請(qǐng)說(shuō)明理由;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)在BC上存在點(diǎn)F,當(dāng)![]() 時(shí),有
時(shí),有![]() 平面PAB.(2)
平面PAB.(2)![]()
【解析】
(1)根據(jù)條件可得![]() 、
、![]() 、
、![]() 兩兩垂直,以
兩兩垂直,以![]() 為原點(diǎn)建立坐標(biāo)系,設(shè)
為原點(diǎn)建立坐標(biāo)系,設(shè)![]() ,從而得到
,從而得到![]() ,若
,若![]() 平面
平面![]() ,則
,則![]() 與平面
與平面![]() 的法向量垂直,從而得到關(guān)于
的法向量垂直,從而得到關(guān)于![]() 的方程,得到
的方程,得到![]() 的值,確定出
的值,確定出![]() 的位置;
的位置;
(2)利用空間向量求出平面![]() ,平面
,平面![]() 的法向量,根據(jù)向量夾角公式,得到兩平面法向量的夾角,從而得到二面角
的法向量,根據(jù)向量夾角公式,得到兩平面法向量的夾角,從而得到二面角![]() 的大小.
的大小.
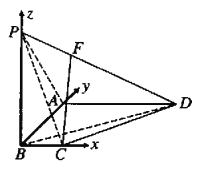
(1)∵![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
∴![]() ,
,![]()
又![]() ,
,
∴![]() ,
,
則可以![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,
建立如圖所示的空間直角坐標(biāo)系,
假設(shè)在PD上存在一點(diǎn)F,使得![]() 平面PAB,
平面PAB,
設(shè)![]() ,
,
由![]() ,得
,得![]() ,
,
由![]() 可得
可得![]() ,
,
又![]() ,故
,故![]() .
.
因?yàn)?/span>![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]()
所以![]() 平面
平面![]() ,
,
故可取平面PAB的一個(gè)法向量為![]() ,
,
若![]() 平面PAB,則
平面PAB,則![]() ,解得
,解得![]() ,
,
故在BC上存在點(diǎn)F,當(dāng)![]() 時(shí),有
時(shí),有![]() 平面PAB.
平面PAB.
(2)由(1)可知![]()
∴![]()
設(shè)平面PAD的法向量![]()
則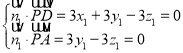 ,
,
令![]() ,則
,則![]() ,
,
此時(shí)![]()
設(shè)平面PBD的法向量![]()
則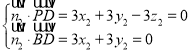 ,
,
令![]() ,則
,則![]()
此時(shí)![]()
∴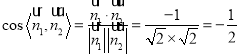 ,
,
∴![]()
∵二面角![]() 為銳二面角,
為銳二面角,
∴二面角![]() 的大小為
的大小為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知四棱錐P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中點(diǎn).

(Ⅰ)求證:PC∥平面EBD;
(Ⅱ)求證:平面PBC⊥平面PCD.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在四棱臺(tái)![]() 中,
中,![]() 底面
底面![]() ,四邊形
,四邊形![]() 為菱形,
為菱形,![]() ,
,![]() .
.
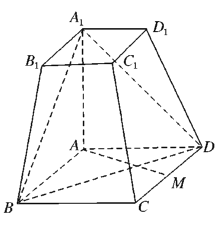
(1)若![]() 為
為![]() 中點(diǎn),求證:
中點(diǎn),求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在直三棱柱![]() 中,平面
中,平面![]() 側(cè)面
側(cè)面![]() ,且
,且![]()
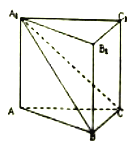
(1)求證: ![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,請(qǐng)問(wèn)在線段
,請(qǐng)問(wèn)在線段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ,請(qǐng)說(shuō)明理由.
,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 與
與![]() 的圖象在點(diǎn)
的圖象在點(diǎn)![]() 處有相同的切線.
處有相同的切線.
(Ⅰ)若函數(shù)![]() 與
與![]() 的圖象有兩個(gè)交點(diǎn),求實(shí)數(shù)
的圖象有兩個(gè)交點(diǎn),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)設(shè)函數(shù)![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市春節(jié)期間7家超市的廣告費(fèi)支出![]() (萬(wàn)元)和銷售額
(萬(wàn)元)和銷售額![]() (萬(wàn)元)數(shù)據(jù)如下:
(萬(wàn)元)數(shù)據(jù)如下:

(1)若用線性回歸模型擬合![]() 與
與![]() 的關(guān)系,求
的關(guān)系,求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)用二次函數(shù)回歸模型擬合![]() 與
與![]() 的關(guān)系,可得回歸方程:
的關(guān)系,可得回歸方程: ![]() ,計(jì)算二次函數(shù)回歸模型和線性回歸模型的
,計(jì)算二次函數(shù)回歸模型和線性回歸模型的![]() 分別約為0.75和0.97,請(qǐng)用
分別約為0.75和0.97,請(qǐng)用![]() 說(shuō)明選擇個(gè)回歸模型更合適,并用此模型預(yù)測(cè)
說(shuō)明選擇個(gè)回歸模型更合適,并用此模型預(yù)測(cè)![]() 超市廣告費(fèi)支出為8萬(wàn)元時(shí)的銷售額.
超市廣告費(fèi)支出為8萬(wàn)元時(shí)的銷售額.
參考數(shù)據(jù):  .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知等差數(shù)列{an}的公差d≠0,且a1,a3,a13成等比數(shù)列,若a1=1,Sn為數(shù)列{an}的前n項(xiàng)和,則![]() 的最小值為( )
的最小值為( )
A.4B.3C.![]() D.2
D.2
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD為直角梯形,PA=AD=DC=2,AB=4且AB∥CD,∠BAD=90°.
(1)求證:BC⊥PC;
(2)求PB與平面PAC所成角的正弦值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了打好脫貧攻堅(jiān)戰(zhàn),某貧困縣農(nóng)科院針對(duì)玉米種植情況進(jìn)行調(diào)研,力爭(zhēng)有效的改良玉米品種,為農(nóng)民提供技術(shù)支.現(xiàn)對(duì)已選出的一組玉米的莖高進(jìn)行統(tǒng)計(jì),獲得莖葉圖如右圖(單位:厘米),設(shè)莖高大于或等于180厘米的玉米為高莖玉米,否則為矮莖玉米.

(1)完成![]() 列聯(lián)表,并判斷是否可以在犯錯(cuò)誤的概率不超過(guò)1%的前提下,認(rèn)為抗倒伏與玉米矮莖有關(guān)?
列聯(lián)表,并判斷是否可以在犯錯(cuò)誤的概率不超過(guò)1%的前提下,認(rèn)為抗倒伏與玉米矮莖有關(guān)?
(2)①按照分層抽樣的方式,在上述樣本中,從易倒伏和抗倒伏兩組中抽取9株玉米,設(shè)取出的易倒伏矮莖玉米株數(shù)為![]() ,求
,求![]() 的分布列(概率用組合數(shù)算式表示);
的分布列(概率用組合數(shù)算式表示);
②若將頻率視為概率,從抗倒伏的玉米試驗(yàn)田中再隨機(jī)抽取出50株,求取出的高莖玉米株數(shù)的數(shù)學(xué)期望和方差.


查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com