【題目】如圖是某商場2018年洗衣機(jī)、電視機(jī)和電冰箱三種電器各季度銷量的百分比堆積圖（例如：第3季度內(nèi)，洗衣機(jī)銷量約占
，電視機(jī)銷量約占
，電冰箱銷量約占
）.根據(jù)該圖，以下結(jié)論中一定正確的是（ ）
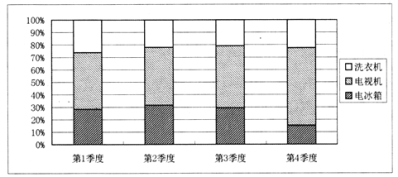
A. 電視機(jī)銷量最大的是第4季度
B. 電冰箱銷量最小的是第4季度
C. 電視機(jī)的全年銷量最大
D. 電冰箱的全年銷量最大
培優(yōu)好卷單元加期末卷系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】在直三棱柱
中，底面
是直角三角形，
，
為側(cè)棱
的中點.
（1）求異面直線
、
所成角的余弦值；
（2）求二面角
的平面角的余弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知兩個無窮數(shù)列
分別滿足
，
，
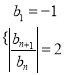其中
，設(shè)數(shù)列的前
項和分別為
，
（1）若數(shù)列都為遞增數(shù)列，求數(shù)列的通項公式；
（2）若數(shù)列
滿足：存在唯一的正整數(shù)
（
），使得
，稱數(shù)列為“墜點數(shù)列”
①若數(shù)列
為“5墜點數(shù)列”，求
；
②若數(shù)列為“
墜點數(shù)列”，數(shù)列
為“
墜點數(shù)列”，是否存在正整數(shù)
，使得
，若存在，求的最大值；若不存在，說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
，（其中
為自然對數(shù)的底數(shù)，
…）.
（1）當(dāng)
時，求函數(shù)
的極值；
（2）若函數(shù)
在區(qū)間
上單調(diào)遞增，求
的取值范圍；
（3）若
，當(dāng)
時，
恒成立，求實數(shù)的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)
的定義域為
，函數(shù)
.
（1）若
時，
的解集為
，求
；
（2）若存在
使得不等式
成立，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
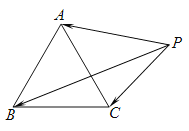
【題目】如圖，
是邊長為1的正三角形，點P在所在的平面內(nèi)，且
（a為常數(shù)），下列結(jié)論中正確的是（ ）
A.當(dāng)
時，滿足條件的點P有且只有一個
B.當(dāng)
時，滿足條件的點P有三個
C.當(dāng)
時，滿足條件的點P有無數(shù)個
D.當(dāng)a為任意正實數(shù)時，滿足條件的點總是有限個
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
，
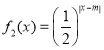，其中
．
（1）若
，令函數(shù)
，解不等式
；
（2）若
，
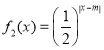，求的值域；
（3）設(shè)函數(shù)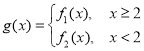
，若對于任意大于等于2的實數(shù)
，總存在唯一的小于2的實數(shù)
，使得
成立，試確定實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
為正整數(shù)且
，將等式
記為
式.
（1）求函數(shù)
，
的值域；
（2）試判斷當(dāng)
時（或2時），是否存在
，
（或，，
）使式成立，若存在，寫出對應(yīng)，（或，，），若不存在，說明理由；
（3）求所有能使式成立的
（
）所組成的有序?qū)崝?shù)對
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，在長方體
中，已知
，
．
（1）求：凸多面體
的體積；
（2）若
為線段
的中點，求點到平面
的距離；
（3）若點
、
分別在棱
、
上滑動，且線段
的長恒等于
，線段的中點為
①試證：點必落在過線段的中點且平行于底面
的平面上；
②試求點的軌跡．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
