
【題目】已知圓C1:x2+y2-2mx-4my+5m2-4=0(m∈R),圓C2:x2+y2=1.
(1)過定點M(1,-2)作圓C2的切線,求切線的方程;
(2)若圓C1與圓C2相交,求m的取值范圍;
(3)已知點P(2,0),圓C1上一點A,圓C2上一點B,求|![]() |的最小值的取值范圍.
|的最小值的取值范圍.
【答案】(1)x=1或3x+4y+5=0;(2)![]() <m<
<m<![]() ;(3)[
;(3)[![]() ,+∞)
,+∞)
【解析】
(1)當(dāng)切線斜率不存在時,切線方程為x=1;當(dāng)切線斜率存在時,設(shè)切線方程為y+2=k(x﹣1),由圓心到直線的距離等于半徑求得k,則切線方程可求;
(2)由圓C1求得C1(m,2m),r1=2,再求得C2(0,0),r2=1,由圓C1與圓C2相交,得r1﹣r2<|C1C2|<r1+r2,由此可得實數(shù)m的范圍;
(3)由題意![]() (﹣2,0)+(m﹣2,2m)
(﹣2,0)+(m﹣2,2m)![]() ,求得
,求得![]() 與
與![]() 共線時
共線時![]() 的范圍為[1,3],而
的范圍為[1,3],而![]() ,其最小值為
,其最小值為![]() ,由此可得當(dāng)向量
,由此可得當(dāng)向量![]() 與
與![]() 共線同向且
共線同向且![]() 與
與![]() 反向時,|
反向時,|![]() |的最小值最小,答案可求.
|的最小值最小,答案可求.
(1)當(dāng)切線斜率不存在時,切線方程為x=1;
當(dāng)切線斜率存在時,設(shè)切線方程為y+2=k(x-1),即kx-y-k-2=0.
由![]() ,解得k=-
,解得k=-![]() ,此時切線方程為3x+4y+5=0.
,此時切線方程為3x+4y+5=0.
∴切線方程為x=1或3x+4y+5=0;
(2)由圓C1:x2+y2-2mx-4my+5m2-4=0,得(x-m)2+(y-2m)2=4,
則C1(m,2m),r1=2,C2(0,0),r2=1.
由圓C1與圓C2相交,得r1-r2<|C1C2|<r1+r2,
∴1![]() ,即
,即![]() <m<
<m<![]() ;
;
(3)如圖,O(0,0),C1(m,2m),P(2,0),
則![]() =
=![]() =(-2,0)+(m-2,2m)+
=(-2,0)+(m-2,2m)+![]()
=(m-4,2m)+![]() ,
,
∵![]() 與
與![]() 共線,∴
共線,∴![]() 的范圍為[1,3],
的范圍為[1,3],
而![]() =
=![]() ,
,
其最小值為![]() ,
,
∴當(dāng)向量![]() 與
與![]() 共線同向且
共線同向且![]() 與
與![]() 反向時,|
反向時,|![]() |的最小值最小,為
|的最小值最小,為![]() ,
,
∴|![]() |的最小值的取值范圍是[
|的最小值的取值范圍是[![]() ,+∞).
,+∞).


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)點P是函數(shù)![]() 圖象上任意一點,點Q坐標(biāo)為
圖象上任意一點,點Q坐標(biāo)為![]() ,當(dāng)
,當(dāng)![]() 取得最小值時圓
取得最小值時圓![]() 與圓
與圓![]() 相外切,則
相外切,則![]() 的最大值為
的最大值為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,離心率
,離心率![]() .
.
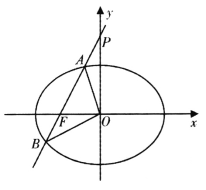
(I)求橢圓C的標(biāo)準(zhǔn)方程;
(II)已知直線![]() 交橢圓C于A,B兩點.
交橢圓C于A,B兩點.
①若直線![]() 經(jīng)過橢圓C的左焦點F,交y軸于點P,且滿足
經(jīng)過橢圓C的左焦點F,交y軸于點P,且滿足![]() .求證:
.求證:![]() 為定值;
為定值;
②若![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為正的常數(shù),函數(shù)
為正的常數(shù),函數(shù)![]() .
.
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)設(shè)![]() ,求
,求![]() 在區(qū)間
在區(qū)間![]() 上的最小值.(
上的最小值.(![]() 為自然對數(shù)的底數(shù))
為自然對數(shù)的底數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知圓![]() 與
與![]() 軸的左右交點分別為
軸的左右交點分別為![]() ,與
,與![]() 軸正半軸的交點為
軸正半軸的交點為![]() .
.
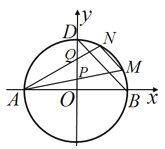
(1)若直線![]() 過點
過點![]() 并且與圓
并且與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若點![]() 是圓
是圓![]() 上第一象限內(nèi)的點,直線
上第一象限內(nèi)的點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是線段
是線段![]() 的中點,直線
的中點,直線![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的離心率為
)的離心率為![]() ,短軸端點到焦點的距離為
,短軸端點到焦點的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() ,
,![]() 為橢圓
為橢圓![]() 上任意兩點,
上任意兩點,![]() 為坐標(biāo)原點,且
為坐標(biāo)原點,且![]() .求證:原點
.求證:原點![]() 到直線
到直線![]() 的距離為定值,并求出該定值.
的距離為定值,并求出該定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校舉行運動會,其中三級跳遠(yuǎn)的成績在8.0米(四舍五入,精確到0.1米)以上的進(jìn)入決賽,把所得數(shù)據(jù)進(jìn)行整理后,分成6組畫出頻率分布直方圖的一部分(如圖),已知從左到右前5個小組的頻率分別為0.04,0.10,0.14,0.28,0.30,第6小組的頻數(shù)是7.

(1)求進(jìn)入決賽的人數(shù);
(2)經(jīng)過多次測試后發(fā)現(xiàn),甲成績均勻分布在8~10米之間,乙成績均勻分布在8.5~10.5米之間,現(xiàn)甲,乙各跳一次,求甲比乙遠(yuǎn)的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com