
【題目】某廠家舉行大型的促銷活動,經測算某產品當促銷費用為x萬元時,銷售量t萬件滿足t=5- ![]() (其中0
(其中0 ![]() x
x ![]() a,a為正常數),現假定生產量與銷售量相等,已知生產該產品t萬件還需投入成本(10+2t)萬元(不含促銷費用),產品的銷售價格定為5+
a,a為正常數),現假定生產量與銷售量相等,已知生產該產品t萬件還需投入成本(10+2t)萬元(不含促銷費用),產品的銷售價格定為5+ ![]() 萬元/萬件.
萬元/萬件.
(1)將該產品的利潤y萬元表示為促銷費用x萬元的函數;
(2)促銷費用投入多少萬元時,廠家的利潤最大.
【答案】
(1)解:由題意知,利潤y=t(5+ ![]() ))﹣(10+2t)﹣x=3t+10-x
))﹣(10+2t)﹣x=3t+10-x
由銷售量t萬件滿足t=5- ![]() (其中0≤x≤a , a為正常數).
(其中0≤x≤a , a為正常數).
代入化簡可得:y=25-( ![]() +x),(0≤x≤a , a為正常數)
+x),(0≤x≤a , a為正常數)
(2)解:由(1)知y =28-( ![]() +x+3)
+x+3) ![]() ,
,
當且僅當 ![]() = x +3,即x =3時,上式取等號.
= x +3,即x =3時,上式取等號.
當a≥3時,促銷費用投入3萬元時,廠家的利潤最大;
當0<a<3時,y在0≤x≤a上單調遞增,
x = a , 函數有最大值.促銷費用投入x = a萬元時,廠家的利潤最大.
綜上述,當a≥3時,促銷費用投入3萬元時,廠家的利潤最大;
當0<a<3時,促銷費用投入x = a萬元時,廠家的利潤最大
【解析】(1)根據題目條件寫出方程,進行化簡即可,要注意自變量x的取值范圍。
(2)先利用均值不等式求出最大值,再根據a的范圍,判斷投入多大時,利潤最大。


科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓Ω: ![]() 的離心率為
的離心率為 ![]() ,直線l:y=2上的點和橢圓Ω上的點的距離的最小值為1.
,直線l:y=2上的點和橢圓Ω上的點的距離的最小值為1.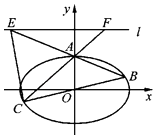
(Ⅰ) 求橢圓Ω的方程;
(Ⅱ) 已知橢圓Ω的上頂點為A,點B,C是Ω上的不同于A的兩點,且點B,C關于原點對稱,直線AB,AC分別交直線l于點E,F.記直線AC與AB的斜率分別為k1 , k2
①求證:k1k2為定值;
②求△CEF的面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】祖暅原理:“冪勢既同,則積不容異”,它是中國古代一個涉及幾何體體積問題,意思是兩個等高的幾何體,如在同高處的截面積恒相等,則體積相等,設A,B為兩個等高的幾何體,p:A,B的體積相等,q:A,B在同高處的截面積不恒相等,根據祖暅原理可知,q是-p的( )
A.充分不必要條件
B.必要不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() .
.
(1)當a>0時,解關于x的不等式f(x)<0;
(2)若當a>0時,f(x)<0在x ![]() [1,2]上恒成立,求實數a的取值范圍.
[1,2]上恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義域為![]() 的函數
的函數![]() 滿足:
滿足:![]() ,且對于任意實數
,且對于任意實數![]() ,
,![]() 恒有
恒有![]() ,當
,當![]() 時,
時,![]() .
.
(1)求![]() 的值,并證明當
的值,并證明當![]() 時,
時,![]() ;
;
(2)判斷函數![]() 在
在![]() 上的單調性并加以證明;
上的單調性并加以證明;
(3)若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
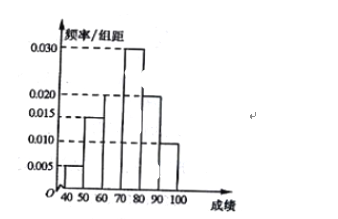
【題目】某中學舉行了數學測試,并從中隨機抽取了60名學生的成績(滿分100分)作為樣本,其中成績不低于80分的學生被評為優秀生,得到成績分布的頻率分布直方圖如圖所示.
(I)若該所中學共有3000名學生,試利用樣本估計全校這次考試中優秀生人數;
(II)若在樣本中,利用分層抽樣的方法從成績不低于70分的學生中隨機抽取6人,再從中抽取3人,試求恰好抽中1名優秀生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
如圖,在四棱錐P—ABCD中,側面PAD⊥底面ABCD,側棱PA=PD=![]() ,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點.
,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點.
(Ⅰ)求證:PO⊥平面ABCD;
(Ⅱ)求異面直線PB與CD所成角的余弦值;
(Ⅲ)求點A到平面PCD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}(n∈N*)滿足:a1=1,an+1-sin2θ·an=cos 2θ·cos2nθ,其中θ∈![]() .
.
(1)當θ=![]() 時,求數列{an}的通項公式;
時,求數列{an}的通項公式;
(2)在(1)的條件下,若數列{bn}滿足bn=sin![]() +cos
+cos![]() (n∈N*,n≥2),且b1=1,求證:對任意的n∈N*,1≤bn≤
(n∈N*,n≥2),且b1=1,求證:對任意的n∈N*,1≤bn≤![]() 恒成立.
恒成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com