
【題目】已知函數![]() .(其中常數
.(其中常數![]() ,是自然對數的底數.)
,是自然對數的底數.)
(1)討論函數![]() 的單調性;
的單調性;
(2)證明:對任意的![]() ,當
,當![]() 時,
時,![]() .
.
【答案】(1)答案不唯一,具體見解析(2)證明見解析
【解析】
(1)求導得![]() ,再分參數當
,再分參數當![]() 和
和![]() 兩種情況具體討論,結合導數正負與原函數關系判斷即可;
兩種情況具體討論,結合導數正負與原函數關系判斷即可;
(2)解法不唯一,由![]() 原不等式可等價轉化為
原不等式可等價轉化為![]() ,采用構造函數法,設
,采用構造函數法,設![]() ,則
,則![]() ,當
,當![]() 時,
時,![]() ,可設
,可設![]() ,求導判斷可知
,求導判斷可知![]() ,進而得出當
,進而得出當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
∴![]() ,從而得證;還可采用合并參數形式得
,從而得證;還可采用合并參數形式得![]() ,令
,令![]() ,討論
,討論![]() 可判斷
可判斷![]() ,當
,當![]() 時,
時,![]() 顯然成立;當
顯然成立;當![]() 且
且![]() 時,
時,![]() ,要證對任意的
,要證對任意的![]() ,
,![]() 成立,只需證
成立,只需證![]() ,可化為
,可化為![]() ,令
,令![]() ,通過討論
,通過討論![]() 確定函數極值點進而得證;其余證法詳見解析
確定函數極值點進而得證;其余證法詳見解析
(1)![]() .
.
①當![]() 時,
時,![]() ,函數
,函數![]() 在R上單調遞增;
在R上單調遞增;
②當![]() 時,由
時,由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() .
.
故![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
綜上所述,當![]() 時,
時,![]() 在R上單調遞增;
在R上單調遞增;
當![]() 時,
時,![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)證法一:原不等式等價于![]()
令![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,
,
令![]() ,則當
,則當![]() 時,
時,![]() ,
,
∴當![]() 時,
時,![]() 單調遞增,即
單調遞增,即![]() ,
,
∴當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
∴![]()
即![]() ,故
,故![]() .
.
證法二:原不等式等價于![]() .
.
令![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
∴![]() ,即
,即![]() ,當且僅當
,當且僅當![]() 時等號成立.
時等號成立.
當![]() 時,
時,![]() 顯然成立;
顯然成立;
當![]() 且
且![]() 時,
時,![]() .
.
欲證對任意的![]() ,
,![]() 成立,只需證
成立,只需證![]()
思路1:∵![]() ,∴不等式
,∴不等式![]() 可化為
可化為![]() ,
,
令![]() ,則
,則![]() ,
,
易證當![]() 時,
時,![]() ,
,
∴當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
∴函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴![]()
∴![]() ,即
,即![]() ,
,
從而,對任意的![]() ,當
,當![]() 時,
時,![]() .
.
思路2:令![]() ,則
,則![]() .
.
![]() ,
,![]() 或
或![]()
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
∵![]() ,
,
∴![]() ,即
,即![]() .
.
從而,對任意的![]() ,當
,當![]() 時,
時,![]() .
.
證法三:原不等式等價于![]() .
.
令![]() ,則
,則![]() .
.
令![]() ,則
,則![]() ,其中
,其中![]() .
.
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增.
上單調遞增.
注意到![]() ,故當
,故當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
∴![]() ,即
,即![]() .
.
②當![]() 時,
時,![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
②(i):若![]() ,則
,則![]() .
.
∵![]()
∴當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
與①同,不等式成立.
②(ii):若![]() ,則
,則![]() ,
,
∵![]()
∴![]() ,使得
,使得![]() ,且當
,且當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
∵![]()
∴此時,![]() ,即
,即![]() .
.
綜上所述,結論得證


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案科目:高中數學 來源: 題型:
【題目】已知△ABC三內角A、B、C所對邊的長分別為a,b,c,且3sin2A+3sin2B=4sinAsinB+3sin2C.
(1)求cosC的值;
(2)若a=3,c![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
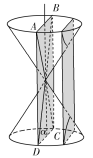
【題目】古希臘數學家阿波羅尼斯在他的著作《圓錐曲線論》中記載了用平面切割圓錐得到圓錐曲線的方法.如圖,將兩個完全相同的圓錐對頂放置(兩圓錐的軸重合),已知兩個圓錐的底面半徑均為1,母線長均為3,記過圓錐軸的平面![]() 為平面
為平面![]() (
(![]() 與兩個圓錐側面的交線為
與兩個圓錐側面的交線為![]() ),用平行于
),用平行于![]() 的平面截圓錐,該平面與兩個圓錐側面的交線即雙曲線
的平面截圓錐,該平面與兩個圓錐側面的交線即雙曲線![]() 的一部分,且雙曲線
的一部分,且雙曲線![]() 的兩條漸近線分別平行于
的兩條漸近線分別平行于![]() ,則雙曲線
,則雙曲線![]() 的離心率為( )
的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() 點
點![]() 是橢圓上任意一點,且
是橢圓上任意一點,且![]() 的最大值為4,橢圓
的最大值為4,橢圓![]() 的離心率與雙曲線
的離心率與雙曲線![]() 的離心率互為倒數.
的離心率互為倒數.
(1)求橢圓方程;
(2)設點![]() ,過點
,過點![]() 作直線
作直線![]() 與圓
與圓![]() 相切且分別交橢圓于
相切且分別交橢圓于![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的焦距為
的焦距為![]() ,斜率為
,斜率為![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點,若線段
兩點,若線段![]() 的中點為
的中點為![]() ,且直線
,且直線![]() 的斜率為
的斜率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若過左焦點![]() 斜率為
斜率為![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]()
![]() 為橢圓上一點,且滿足
為橢圓上一點,且滿足![]() ,問:
,問:![]() 是否為定值?若是,求出此定值,若不是,說明理由.
是否為定值?若是,求出此定值,若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要得到![]() 的圖象
的圖象![]() ,只要將
,只要將![]() 圖象
圖象![]() 怎樣變化得到( )
怎樣變化得到( )
A.將![]() 的圖象
的圖象![]() 沿x軸方向向左平移
沿x軸方向向左平移![]() 個單位
個單位
B.將![]() 的圖象
的圖象![]() 沿x軸方向向右平移
沿x軸方向向右平移![]() 個單位
個單位
C.先作![]() 關于x軸對稱圖象
關于x軸對稱圖象![]() ,再將圖象
,再將圖象![]() 沿x軸方向向右平移
沿x軸方向向右平移![]() 個單位
個單位
D.先作![]() 關于x軸對稱圖象
關于x軸對稱圖象![]() ,再將圖象
,再將圖象![]() 沿x軸方向向左平移
沿x軸方向向左平移![]() 個單位
個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)證明:![]() 為等比數列,求出
為等比數列,求出![]() 的通項公式;
的通項公式;
(2)若![]() ,求
,求![]() 的前n項和
的前n項和![]() ,并判斷是否存在正整數n使得
,并判斷是否存在正整數n使得![]() 成立?若存在求出所有n值;若不存在說明理由.
成立?若存在求出所有n值;若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2017年1月至2019年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論正確的是( )
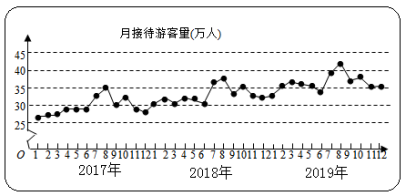
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位數為30
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com