
【題目】如圖所示,該幾何體是由一個直三棱柱ABE﹣DCF和一個四棱錐P﹣ABCD組合而成,其中EF=EA=EB=2,AE⊥EB,PA=PD![]() ,平面PAD∥平面EBCF.
,平面PAD∥平面EBCF.
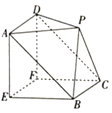
(1)證明:平面PBC∥平面AEFD;
(2)求直線AP與平面PCD所成角的正弦值.
【答案】(1)見解析(2)![]() .
.
【解析】
(1)取EF中點O,BC中點G,AD中點H,連結OH,PH,OG,PG,證明OH∥PG,AD∥BC,故得證.
(2)以O為原點,OE為x軸,OG為y軸,OH為z軸,建立空間直角坐標系,計算平面PCD的法向量,借助線面角的向量公式即得解.
證明:取EF中點O,BC中點G,AD中點H,連結OH,PH,OG,PG,
![]()
由題意得PH![]() 2=OH=OG,
2=OH=OG,
∴PH![]() OG,∴四邊形PHOG是平行四邊形,∴OH∥PG,
OG,∴四邊形PHOG是平行四邊形,∴OH∥PG,
∵AB![]() DC,∴四邊形ABCD是平行四邊形,∴AD∥BC,
DC,∴四邊形ABCD是平行四邊形,∴AD∥BC,
∵AD∩OH=H,BC∩PG=G,
∴平面PBC∥平面AEFD.
以O為原點,OE為x軸,OG為y軸,OH為z軸,建立空間直角坐標系,
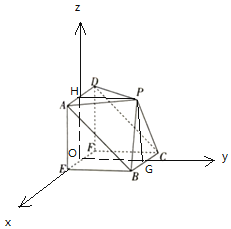
則A(1,0,2),P(0,2,2),C(﹣1,2,0),D(﹣1,0,2),
![]() (1,﹣2,0),
(1,﹣2,0),![]() (﹣1,0,﹣2),
(﹣1,0,﹣2),![]() (﹣1,﹣2,0),
(﹣1,﹣2,0),
設平面PCD的法向量![]() (x,y,z),
(x,y,z),
則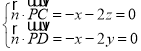 ,取x=2,得
,取x=2,得![]() (2,﹣1,﹣1),
(2,﹣1,﹣1),
設直線AP與平面PCD所成角為θ,
則sinθ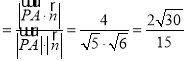 .
.
∴直線AP與平面PCD所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某校要在一條水泥路邊安裝路燈,其中燈桿的設計如圖所示,AB為地面,CD,CE為路燈燈桿,CD⊥AB,∠DCE=![]() ,在E處安裝路燈,且路燈的照明張角∠MEN=
,在E處安裝路燈,且路燈的照明張角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
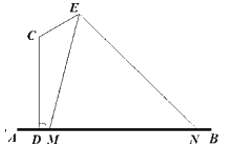
(1)當M,D重合時,求路燈在路面的照明寬度MN;
(2)求此路燈在路面上的照明寬度MN的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 截直線
截直線![]() 所得的線段的長度為
所得的線段的長度為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,點
兩點,點![]() 是橢圓
是橢圓![]() 上的點,
上的點,![]() 是坐標原點,若
是坐標原點,若![]() ,判定四邊形
,判定四邊形![]() 的面積是否為定值?若為定值,求出定值;如果不是,請說明理由.
的面積是否為定值?若為定值,求出定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() (a>0,b>0)的左右焦點分別為F1,F2,與y軸正半軸交于點B,若△BF1F2為等腰直角三角形,且直線BF1被圓x2+y2=b2所截得的弦長為2,
(a>0,b>0)的左右焦點分別為F1,F2,與y軸正半軸交于點B,若△BF1F2為等腰直角三角形,且直線BF1被圓x2+y2=b2所截得的弦長為2,
(1)求橢圓的方程;
(2)直線l:y=kx+m與橢圓交于點A,C,線段AC的中點為M,射線MO與橢圓交于點P,點O為△PAC的重心,求證:△PAC的面積S為定值;
查看答案和解析>>
科目:高中數學 來源: 題型:
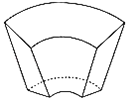
【題目】《九章算術》是我國古代內容極為豐富的數學名著,書中有如下問題:“今有曲池,上中周二丈,外周四丈,廣一丈,下中周一丈四尺,外周二丈四尺,廣五尺,深一丈,問積幾何?”其意思為:“今有上下底面皆為扇形的水池,上底中周2丈,外周4丈,寬1丈;下底中周1丈4尺,外周長2丈4尺,寬5尺;深1丈.問它的容積是多少?”則該曲池的容積為( )立方尺(1丈=10尺,曲池:上下底面皆為扇形的土池,其容積公式為![]() [(2×上寬+下寬)
[(2×上寬+下寬)![]() (2×下寬+上寬)
(2×下寬+上寬)![]() ]×深)
]×深)
A.![]() B.1890C.
B.1890C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若關于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() ,求函數
,求函數![]() 的最小值;
的最小值;
(2)是否存在實數![]() ,使得對任意
,使得對任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立?若存在,求出
成立?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x-a|-![]() x(a>0).
x(a>0).
(1)若a=3,解關于x的不等式f(x)<0;
(2)若對于任意的實數x,不等式f(x)-f(x+a)<a2+![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,已知直線l1的參數方程為![]() (t為參數),直線l2的參數方程為
(t為參數),直線l2的參數方程為 (t為參數),其中α∈(0,
(t為參數),其中α∈(0,![]() ),以原點O為點x軸的非負半軸為極軸,取相同的單位長度建立極坐標系,曲線C的極坐標方程為ρ﹣2sinθ=0.
),以原點O為點x軸的非負半軸為極軸,取相同的單位長度建立極坐標系,曲線C的極坐標方程為ρ﹣2sinθ=0.
(1)寫出直線l1的極坐標方程和曲線C的直角坐標方程;
(2)設直線l1,l2分別與曲線C交于點A,B(非坐標原點)求|AB|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com