【題目】已知兩個不相等的非零向量
，兩組向量
和
均由2個
和3個
排列而成，記
，
表示
所有可能取值中的最小值，則下列命題中
（1）有5個不同的值；（2）若
則與
無關；（3）若
，則與
無關；（4）若
，則
；（5）若
，
，則與的夾角為
．正確的是（ ）
A.（1）（2）B.（2）（4）C.（3）（5）D.（1）（4）
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】對于數列
，稱
（其中
）為數列的前k項“波動均值”.若對任意的，都有
，則稱數列為“趨穩數列”．
（1）若數列1，
，2為“趨穩數列”，求的取值范圍；
（2）若各項均為正數的等比數列
的公比
，求證：是“趨穩數列”；
（3）已知數列的首項為1，各項均為整數，前
項的和為
. 且對任意，都有
， 試計算：
（
）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
是定義在
上的函數，如果存在常數
，對區間的任意劃分：
，和式
恒成立，則稱為上的“絕對差有界函數”。注：
。
（1）證明函數
在
上是“絕對差有界函數”。
（2）證明函數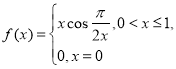
不是
上的“絕對差有界函數”。
（3）記集合
存在常數
，對任意的
，有
成立
，證明集合
中的任意函數為“絕對差有界函數”，并判斷
是否在集合中，如果在，請證明并求
的最小值；如果不在，請說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左焦點為F，短軸的兩個端點分別為A，B，且
，
為等邊三角形.
（1）求橢圓C的方程；
（2）如圖，點M在橢圓C上且位于第一象限內，它關于坐標原點O的對稱點為N；過點M作x軸的垂線，垂足為H，直線
與橢圓C交于另一點J，若
，試求以線段
為直徑的圓的方程；
（3）已知
是過點A的兩條互相垂直的直線，直線
與圓
相交于P，Q兩點，直線
與橢圓C交于另一點R，求
面積最大值時，直線的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業在“精準扶貧”行動中，決定幫助一貧困山區將水果運出銷售.現有8輛甲型車和4輛乙型車，甲型車每次最多能運6噸且每天能運4次，乙型車每次最多能運10噸且每天能運3次，甲型車每天費用320元，乙型車每天費用504元．若需要一天內把180噸水果運輸到火車站，則通過合理調配車輛，運送這批水果的費用最少為（ ）
A.2400元B.2560元C.2816元D.4576元
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某電視臺舉行一個比賽類型的娛樂節目，
兩隊各有六名選手參賽，將他們首輪的比賽成績作為樣本數據，繪制成莖葉圖如圖所示，為了增加節目的趣味性，主持人故意將
隊第六位選手的成績沒有給出，并且告知大家
隊的平均分比隊的平均分多4分，同時規定如果某位選手的成績不少于21分，則獲得“晉級”.
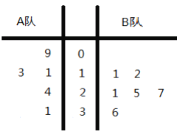
（1）主持人從隊所有選手成績中隨機抽取2個，求至少有一個為“晉級”的概率；
（2）主持人從兩隊所有選手成績中分別隨機抽取2個，記抽取到“晉級”選手的總人數為
，求的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某甲
籃球隊的12名隊員（含2名外援）中有5名主力隊員（含一名外援），主教練要從12名隊員中選5人首發上場，則主力隊員不少于4人，且有一名外援上場的概率是_____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數
和函數
,
（1）若
為偶函數,試判斷
的奇偶性;
（2）若方程
有兩個不等的實根
,則
①試判斷函數在區間
上是否具有單調性,并說明理由;
②若方程
的兩實根為
求使
成立的
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱ABC-
中，
平面ABC，D，E，F，G分別為
，AC，
，
的中點，AB=BC=
，AC==2．
（Ⅰ）求證：AC⊥平面BEF；
（Ⅱ）求二面角B-CD-C1的余弦值；
（Ⅲ）證明：直線FG與平面BCD相交．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
