Question

【題目】已知點A（﹣1，0），B（1，0），C（0，1），直線y＝ax+b（a＞0）將△ABC分割為面積相等的兩部分，則b的取值范圍是（　　）

A.（0，1）B.C.D.

Answer 1

【答案】B

【解析】

先求得直線y＝ax+b（a＞0）與x軸的交點為M（，0），由0可得點M在射線OA上．求出直線和BC的交點N的坐標，①若點M和點A重合，求得b；②若點M在點O和點A之間，求得b； ③若點M在點A的左側，求得b＞1．再把以上得到的三個b的范圍取并集，可得結果．

由題意可得，三角形ABC的面積為 1，

由于直線y＝ax+b（a＞0）與x軸的交點為M（，0），

由直線y＝ax+b（a＞0）將△ABC分割為面積相等的兩部分，可得b＞0，

故0，故點M在射線OA上．

設直線y＝ax+b和BC的交點為N，則由可得點N的坐標為（，）．

①若點M和點A重合，如圖：

則點N為線段BC的中點，故N（，），

把A、N兩點的坐標代入直線y＝ax+b，求得a＝b．

②若點M在點O和點A之間，如圖：

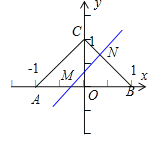
此時b，點N在點B和點C之間，

由題意可得三角形NMB的面積等于，

即，即 ，可得a0，求得 b，

故有b．

③若點M在點A的左側，

則b，由點M的橫坐標1，求得b＞a．

設直線y＝ax+b和AC的交點為P，則由 求得點P的坐標為（，），

此時，由題意可得，三角形CPN的面積等于，即 （1﹣b）|xN﹣xP|，

即（1﹣b）||，化簡可得2（1﹣b）2＝|a2﹣1|．

由于此時 b＞a＞0，0＜a＜1，∴2（1﹣b）2＝|a2﹣1|＝1﹣a2 ．

兩邊開方可得 （1﹣b）1，∴1﹣b，化簡可得 b＞1，

故有1b．

綜上可得b的取值范圍應是 ，

故選：B．