
【題目】已知函數![]() 在
在![]() 處有極值10.
處有極值10.
(1)求實數![]() 的值;
的值;
(2)設![]() ,討論函數
,討論函數![]() 在區間
在區間![]() 上的單調性.
上的單調性.
【答案】(1) ![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:
(1)利用導函數與切線之間的關于得到關于實數m,n的方程組,求解方程組即可,注意驗證所得的結果是否符合題意,舍去不合題意的值可得: ![]() ;
;
(2)結合(1)的結論首先確定函數![]() 的其單調性和極值分布,結合函數的定義域分類討論可得:當
的其單調性和極值分布,結合函數的定義域分類討論可得:當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上的單調性為:
上的單調性為:
![]() 時,單調遞減;
時,單調遞減;
![]() 時,
時, ![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
![]() 時,
時, ![]() 在
在![]() 上單調遞增.
上單調遞增.
試題解析:
(1)![]() 定義域為
定義域為![]() ,
,
∵![]() 在
在![]() 處有極值10,
處有極值10,
∴![]() 且
且![]() ,
,
即![]() ,解得:
,解得:  或
或 ,
,
當![]() 時,
時, ![]() ,
,
當![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 處有極值10時,
處有極值10時, ![]() .
.
(2)由(1)可知![]() ,其單調性和極值分布情況如下表:
,其單調性和極值分布情況如下表:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| 增 | 極大 | 減 | 極小 | 增 |
∴①當![]() 且
且![]() ,即
,即![]() 時,
時, ![]() 在區間
在區間![]() 上的單調遞減;
上的單調遞減;
②當![]() ,即
,即![]() 時,
時, ![]() 在區間
在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增;
上單調遞增;
③當![]() 時,
時, ![]() 在區間
在區間![]() 上單調遞增.
上單調遞增.
綜上所述,當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上的單調性為:
上的單調性為:
![]() 時,單調遞減;
時,單調遞減; ![]() 時,
時, ![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增; ![]() 時,
時, ![]() 在
在![]() 上單調遞增.
上單調遞增.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC=2,E是PB上的點. 
(1)求證:平面EAC⊥平面PBC;
(2)若E是PB的中點,求二面角P﹣AC﹣E的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間將10名技工平均分成甲、乙兩組加工某種零件,在單位時間內每個技工加工的合格零件數的統計數據的莖葉圖如圖所示.已知兩組技工在單位時間內加工的合格零件平均數都為9. 
(1)分別求出m,n的值;
(2)分別求出甲、乙兩組技工在單位時間內加工的合格零件的方差 ![]() 和
和 ![]() ,并由此分析兩組技工的加工水平.
,并由此分析兩組技工的加工水平.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+3x2﹣9x+m
(1)求函數f(x)=x3+3x2﹣9x+m的單調遞增區間;
(2)若函數f(x)在區間[0,2]上的最大值12,求函數f(x)在該區間上的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線l過P(1,2),且A(2,3),B(4,﹣5)到l的距離相等,則直線l的方程是( )
A.4x+y﹣6=0
B.x+4y﹣6=0
C.3x+2y﹣7=0或4x+y﹣6=0
D.2x+3y﹣7=0或x+4y﹣6=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是平行四邊形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA= ![]() ,E為BC的中點.
,E為BC的中點. 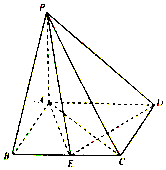
(1)證明:PE⊥ED;
(2)求二面角E﹣PD﹣A的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A,B兩地的距離是120km,按交通法規規定,A,B兩地之間的公路車速應限制在50~100km/h,假設汽油的價格是6元/升,以xkm/h速度行駛時,汽車的耗油率為 ![]() ,司機每小時的工資是36元,那么最經濟的車速是多少?如果不考慮其他費用,這次行車的總費用是多少?
,司機每小時的工資是36元,那么最經濟的車速是多少?如果不考慮其他費用,這次行車的總費用是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com