Question

【題目】某群體的人均通勤時間，是指單日內該群體中成員從居住地到工作地的平均用時．某地上班族中的成員僅以自駕或公交方式通勤．分析顯示：當中（）的成員自駕時，自駕群體的人均通勤時間為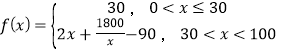（單位：分鐘），而公交群體的人均通勤時間不受影響，恒為分鐘，試根據上述分析結果回答下列問題：

（1）當在什么范圍內時，公交群體的人均通勤時間少于自駕群體的人均通勤時間？

（2）求該地上班族的人均通勤時間的表達式；討論的單調性，并說明其實際意義．

Answer 1

【答案】(1) 時，公交群體的人均通勤時間少于自駕群體的人均通勤時間;(2)見解析.

【解析】

（1）由題意知求出f（x）＞40時x的取值范圍即可；

（2）分段求出g（x）的解析式，判斷g（x）的單調性，再說明其實際意義．

（1）由題意知，當時，

，

即，

解得或，

∴時，公交群體的人均通勤時間少于自駕群體的人均通勤時間；

（2）當時，

；

當時，

；

∴；

當時，單調遞減；

當時，單調遞增；

說明該地上班族中有小于的人自駕時，人均通勤時間是遞減的；

有大于的人自駕時，人均通勤時間是遞增的；

當自駕人數為時，人均通勤時間最少．