
【題目】【2018廣東深圳市高三第一次調研考試】已知函數![]() .
.
(I)討論函數![]() 的單調性;
的單調性;
(II)當![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(I)見解析;(II)![]() .
.
【解析】試題分析:(1)求出![]() 的定義域以及導函數
的定義域以及導函數![]() ,分四種情況討論
,分四種情況討論![]() 的范圍,分別令
的范圍,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間, ![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(2)
的減區間;(2) ![]() ,等價于
,等價于![]() ,討論
,討論![]() 的范圍,利用導數研究函數的單調性,分別令求出函數
的范圍,利用導數研究函數的單調性,分別令求出函數![]() 的最小值,令最小值大于零,可篩選出符合題意的
的最小值,令最小值大于零,可篩選出符合題意的![]() 的取值范圍.
的取值范圍.
試題解析:(1) ![]() 的定義域為
的定義域為![]() .
.
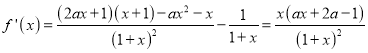 .
.
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() .
.
①當![]() 時,
時, ![]() ,在
,在![]() 時,
時, ![]() ;在
;在![]() 時,
時, ![]() ,
,
所以![]() 在
在![]() 單調遞減,
單調遞減, ![]() 在
在![]() 單調遞增;
單調遞增;
②當![]() 時,
時, ![]() ,在
,在![]() 時,
時, ![]() ;在
;在![]() 時,
時, ![]() ;在
;在![]() 時,
時, ![]() .所以
.所以![]() 在
在![]() ,
, ![]() 單調遞增,
單調遞增, ![]() 在
在![]() 單調遞減;
單調遞減;
③當![]() 時,
時, ![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 單調遞增;
單調遞增;
④當![]() 時,
時, ![]() .在
.在![]() 時,
時, ![]() ;在
;在![]() 時,
時, ![]() ;在
;在![]() 時,
時, ![]() ,所以
,所以![]() 在
在![]() ,
, ![]() 單調遞增,
單調遞增, ![]() 在
在![]() 單調遞減;
單調遞減;
(2)當![]() 時,
時, ![]() ,
, ![]() ,即
,即![]() .
.
設![]() ,
, ![]() ,只需
,只需![]() ,在
,在![]() 上恒成立即可.
上恒成立即可.
因為![]() ,
, ![]() .
.
又![]() ,所以
,所以![]() .
.
令![]() ,得
,得![]() .
.
當![]() 時,
時, ![]() ,在
,在![]() 上
上![]() ,故
,故![]() 單調遞增,
單調遞增,
所以![]() 恒成立;
恒成立;
當![]() 時,
時, ![]() ,即
,即![]() ,故
,故![]() .
.
故當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,此時函數
,此時函數![]() 在
在![]() 上單調遞減.
上單調遞減.
又![]() ,所以在
,所以在![]() 上
上![]() ,與題設矛盾.
,與題設矛盾.
當![]() 時,
時, ![]() ,此時函數
,此時函數![]() 在
在![]() 上單調遞減.
上單調遞減.
又![]() ,所以在
,所以在![]() 上
上![]() ,與題設矛盾.
,與題設矛盾.
綜上, ![]() .
.


科目:高中數學 來源: 題型:
【題目】下列命題中,真命題是( )
A. 設![]() ,則
,則![]() 為實數的充要條件是
為實數的充要條件是![]() 為共軛復數;
為共軛復數;
B. “直線![]() 與曲線C相切”是“直線
與曲線C相切”是“直線![]() 與曲線C只有一個公共點”的充分不必要條件;
與曲線C只有一個公共點”的充分不必要條件;
C. “若兩直線![]() ,則它們的斜率之積等于
,則它們的斜率之積等于![]() ”的逆命題;
”的逆命題;
D. ![]() 是R上的可導函數,“若
是R上的可導函數,“若![]() 是
是![]() 的極值點,則
的極值點,則![]() ”的否命題.
”的否命題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,滿足
上的奇函數,滿足![]() ,當
,當![]() 時,有
時,有![]() .
.
(1)求實數![]() 的值;
的值;
(2)求函數![]() 在區間
在區間![]() 上的解析式,并利用定義證明證明其在該區間上的單調性;
上的解析式,并利用定義證明證明其在該區間上的單調性;
(3)解關于![]() 的不等式
的不等式![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校選派甲、乙、丙、丁、戊5名學生代表學校參加市級“演講”和“詩詞”比賽,下面是他們的一段對話.甲說:“乙參加‘演講’比賽”;乙說:“丙參加‘詩詞’比賽”;丙說“丁參加‘演講’比賽”;丁說:“戊參加‘詩詞’比賽”;戊說:“丁參加‘詩詞’比賽”.
已知這5個人中有2人參加“演講”比賽,有3人參加“詩詞”比賽,其中有2人說的不正確,且參加“演講”的2人中只有1人說的不正確.根據以上信息,可以確定參加“演講”比賽的學生是
A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國數學家科拉茨1937年提出一個著名的猜想:任給一個正整數![]() ,如果
,如果![]() 是偶數,就將它減半(即
是偶數,就將它減半(即![]() );如果
);如果![]() 是奇數,則將它乘3加1(即
是奇數,則將它乘3加1(即![]() ),不斷重復這樣的運算,經過有限步后,一定可以得到1.對于科拉茨猜想,目前誰也不能證明,也不能否定.現在請你研究:如果對正整數
),不斷重復這樣的運算,經過有限步后,一定可以得到1.對于科拉茨猜想,目前誰也不能證明,也不能否定.現在請你研究:如果對正整數![]() (首項)按照上述規則進行變換后的第9項為1(注:1可以多次出現),則
(首項)按照上述規則進行變換后的第9項為1(注:1可以多次出現),則![]() 的所有不同值的個數為( )
的所有不同值的個數為( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小張經營某一消費品專賣店,已知該消費品的進價為每件40元,該店每月銷售量(百件)與銷售單價x(元/件)之間的關系用下圖的一折線表示,職工每人每月工資為1000元,該店還應交付的其它費用為每月10000元.

(1)把y表示為x的函數;
(2)當銷售價為每件50元時,該店正好收支平衡(即利潤為零),求該店的職工人數;
(3)若該店只有20名職工,問銷售單價定為多少元時,該專賣店可獲得最大月利潤?(注:利潤=收入-支出)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com