
【題目】冠狀病毒是一個(gè)大型病毒家族,己知可引起感冒以及中東呼吸綜合征(![]() )和嚴(yán)重急性呼吸綜合征(
)和嚴(yán)重急性呼吸綜合征(![]() )等較嚴(yán)重疾病.而今年出現(xiàn)在湖北武漢的新型冠狀病毒(
)等較嚴(yán)重疾病.而今年出現(xiàn)在湖北武漢的新型冠狀病毒(![]() )是以前從未在人體中發(fā)現(xiàn)的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發(fā)熱、咳嗽、氣促和呼吸困難等.在較嚴(yán)重病例中,感染可導(dǎo)致肺炎、嚴(yán)重急性呼吸綜合征、腎衰竭,甚至死亡.
)是以前從未在人體中發(fā)現(xiàn)的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發(fā)熱、咳嗽、氣促和呼吸困難等.在較嚴(yán)重病例中,感染可導(dǎo)致肺炎、嚴(yán)重急性呼吸綜合征、腎衰竭,甚至死亡.
某醫(yī)院為篩查冠狀病毒,需要檢驗(yàn)血液是否為陽性,現(xiàn)有n(![]() )份血液樣本,有以下兩種檢驗(yàn)方式:
)份血液樣本,有以下兩種檢驗(yàn)方式:
方式一:逐份檢驗(yàn),則需要檢驗(yàn)n次.
方式二:混合檢驗(yàn),將其中k(![]() 且
且![]() )份血液樣本分別取樣混合在一起檢驗(yàn).
)份血液樣本分別取樣混合在一起檢驗(yàn).
若檢驗(yàn)結(jié)果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗(yàn)一次就夠了,如果檢驗(yàn)結(jié)果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗(yàn),此時(shí)這k份血液的檢驗(yàn)次數(shù)總共為![]() .
.
假設(shè)在接受檢驗(yàn)的血液樣本中,每份樣本的檢驗(yàn)結(jié)果是陽性還是陰性都是獨(dú)立的,且每份樣本是陽性結(jié)果的概率為p(![]() ).現(xiàn)取其中k(
).現(xiàn)取其中k(![]() 且
且![]() )份血液樣本,記采用逐份檢驗(yàn)方式,樣本需要檢驗(yàn)的總次數(shù)為
)份血液樣本,記采用逐份檢驗(yàn)方式,樣本需要檢驗(yàn)的總次數(shù)為![]() ,采用混合檢驗(yàn)方式,樣本需要檢驗(yàn)的總次數(shù)為
,采用混合檢驗(yàn)方式,樣本需要檢驗(yàn)的總次數(shù)為![]() .
.
(1)若![]() ,試求p關(guān)于k的函數(shù)關(guān)系式
,試求p關(guān)于k的函數(shù)關(guān)系式![]() ;
;
(2)若p與干擾素計(jì)量![]() 相關(guān),其中
相關(guān),其中![]() (
(![]() )是不同的正實(shí)數(shù),
)是不同的正實(shí)數(shù),
滿足![]() 且
且![]() (
(![]() )都有
)都有![]() 成立.
成立.
(i)求證:數(shù)列![]() 等比數(shù)列;
等比數(shù)列;
(ii)當(dāng)![]() 時(shí),采用混合檢驗(yàn)方式可以使得樣本需要檢驗(yàn)的總次數(shù)的期望值比逐份檢驗(yàn)的總次數(shù)的期望值更少,求k的最大值
時(shí),采用混合檢驗(yàn)方式可以使得樣本需要檢驗(yàn)的總次數(shù)的期望值比逐份檢驗(yàn)的總次數(shù)的期望值更少,求k的最大值
【答案】(1)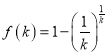 ,(
,(![]() ,且
,且![]() ).(2)(i)見解析(ii)最大值為4.
).(2)(i)見解析(ii)最大值為4.
【解析】
(1)由題設(shè)可知![]() ,
,![]() 的所有可能取值為1,
的所有可能取值為1,![]() ,求
,求![]() ,再根據(jù)
,再根據(jù)![]() ,求
,求![]() ;
;
(2)(ⅰ)當(dāng)![]() 時(shí),
時(shí),![]() ,∴
,∴![]() ,令
,令![]() ,則
,則![]() ,
,
利用數(shù)學(xué)歸納法證明![]() ;
;
(ⅱ)由(ⅰ)可知![]() ,由
,由![]() 可知
可知![]() ,再設(shè)函數(shù)
,再設(shè)函數(shù)![]() (
(![]() ),利用函數(shù)的單調(diào)性求
),利用函數(shù)的單調(diào)性求![]() 的最大值.
的最大值.
(1)解:由已知,![]() ,
,![]() ,得
,得![]() ,
,
![]() 的所有可能取值為1,
的所有可能取值為1,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
若![]() ,則
,則![]() ,
,![]() ,∴
,∴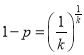 ,∴
,∴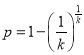 .
.
∴p關(guān)于k的函數(shù)關(guān)系式為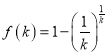 ,(
,(![]() ,且
,且![]() ).
).
(2)(i)∵證明:當(dāng)![]() 時(shí),
時(shí),![]() ,∴
,∴![]() ,令
,令![]() ,則
,則![]() ,
,
∵![]() ,∴下面證明對任意的正整數(shù)n,
,∴下面證明對任意的正整數(shù)n,![]() .
.
①當(dāng)![]() ,2時(shí),顯然成立;
,2時(shí),顯然成立;
②假設(shè)對任意的![]() 時(shí),
時(shí),![]() ,下面證明
,下面證明![]() 時(shí),
時(shí),![]() ;
;
由題意,得![]() ,∴
,∴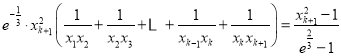 ,
,
∴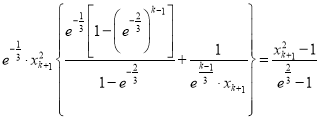 ,
,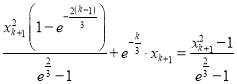 ,
,
∴ ,
,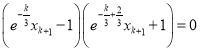 .
.
∴![]() 或
或![]() (負(fù)值舍去).∴
(負(fù)值舍去).∴![]() 成立.
成立.
∴由①②可知,![]() 為等比數(shù)列,
為等比數(shù)列,![]() .
.
(ii)解:由(i)知,![]() ,
,![]() ,∴
,∴![]() ,得
,得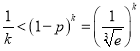 ,∴
,∴![]() .
.
設(shè)![]() (
(![]() ),
),![]() ,∴當(dāng)
,∴當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() 在
在![]() 上單調(diào)減.
上單調(diào)減.
又![]() ,
,![]() ,∴
,∴![]() ;
;![]() ,
,![]() .∴
.∴![]() .
.
∴k的最大值為4.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 的參數(shù)方程為
的參數(shù)方程為![]() (其中
(其中![]() 為參數(shù)),以原點(diǎn)為極點(diǎn),
為參數(shù)),以原點(diǎn)為極點(diǎn),![]() 軸非負(fù)半軸為極軸建立極坐標(biāo)系,則曲線
軸非負(fù)半軸為極軸建立極坐標(biāo)系,則曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求圓![]() 的普通方程與
的普通方程與![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)點(diǎn)![]() 是曲線
是曲線![]() 上一點(diǎn),由
上一點(diǎn),由![]() 向圓
向圓![]() 引切線,切點(diǎn)分別為
引切線,切點(diǎn)分別為![]() ,求四邊形
,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某人某天的工作是駕車從![]() 地出發(fā),到
地出發(fā),到![]() 兩地辦事,最后返回
兩地辦事,最后返回![]() 地,
地,![]() ,三地之間各路段行駛時(shí)間及擁堵概率如下表
,三地之間各路段行駛時(shí)間及擁堵概率如下表
路段 | 正常行駛所用時(shí)間(小時(shí)) | 上午擁堵概率 | 下午擁堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到擁堵,則在該路段行駛時(shí)間需要延長1小時(shí).
現(xiàn)有如下兩個(gè)方案:
方案甲:上午從![]() 地出發(fā)到
地出發(fā)到![]() 地辦事然后到達(dá)
地辦事然后到達(dá)![]() 地,下午從
地,下午從![]() 地辦事后返回
地辦事后返回![]() 地;
地;
方案乙:上午從![]() 地出發(fā)到
地出發(fā)到![]()
![]() 地出發(fā)到達(dá)
地出發(fā)到達(dá)![]() 地,辦完事后返回
地,辦完事后返回![]() 地.
地.
(1)若此人早上8點(diǎn)從![]() 地出發(fā),在各地辦事及午餐的累積時(shí)間為2小時(shí),且采用方案甲,求他當(dāng)日18點(diǎn)或18點(diǎn)之前能返回
地出發(fā),在各地辦事及午餐的累積時(shí)間為2小時(shí),且采用方案甲,求他當(dāng)日18點(diǎn)或18點(diǎn)之前能返回![]() 地的概率.
地的概率.
(2)甲乙兩個(gè)方案中,哪個(gè)方案有利于辦完事后更早返回![]() 地?請說明理由.
地?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)a﹤0時(shí),證明![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 實(shí)數(shù)
實(shí)數(shù)![]() 滿足
滿足![]() ,其中
,其中![]() .
.![]() 實(shí)數(shù)
實(shí)數(shù)![]() 滿足
滿足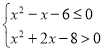 .
.
(1)若![]() ,且
,且![]() 為真,求實(shí)數(shù)
為真,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)非![]() 是非
是非![]() 的充分不必要條件,求實(shí)數(shù)
的充分不必要條件,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 單調(diào)區(qū)間與極值;
單調(diào)區(qū)間與極值;
(2)當(dāng)函數(shù)![]() 有兩個(gè)極值點(diǎn)時(shí),求實(shí)數(shù)
有兩個(gè)極值點(diǎn)時(shí),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某市管轄的海域內(nèi)有一圓形離岸小島,半徑為1公里,小島中心O到岸邊AM的最近距離OA為2公里.該市規(guī)劃開發(fā)小島為旅游景區(qū),擬在圓形小島區(qū)域邊界上某點(diǎn)B處新建一個(gè)浴場,在海岸上某點(diǎn)C處新建一家五星級酒店,在A處新建一個(gè)碼頭,且使得AB與AC滿足垂直且相等,為方便游客,再建一條跨海高速通道OC連接酒店和小島,設(shè)![]() .
.
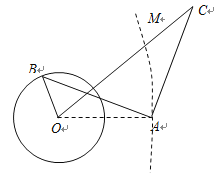
(1)設(shè)![]() ,試將
,試將![]() 表示成
表示成![]() 的函數(shù);
的函數(shù);
(2)若OC越長,景區(qū)的輻射功能越強(qiáng),問當(dāng)![]() 為何值時(shí)OC最長,并求出該最大值.
為何值時(shí)OC最長,并求出該最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸正半軸為極軸,建立極坐標(biāo)系,曲線
軸正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)射線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點(diǎn)(異于原點(diǎn)
兩點(diǎn)(異于原點(diǎn)![]() ),定點(diǎn)
),定點(diǎn)![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com