Question

【題目】已知數列{an}的前n項和為Sn ， 常數λ＞0，且λa1an=S1+Sn對一切正整數n都成立．
（1）求數列{an}的通項公式；
（2）設a1＞0，λ=100，當n為何值時，數列 的前n項和最大？

Answer 1

【答案】
（1）解：當n=1時，

∴a1（λa1﹣2）=0

若取a1=0，則Sn=0，an=Sn﹣Sn﹣1=0

∴an=0（n≥1）

若a1≠0，則 ，當n≥2時，2an= ，

兩式相減可得，2an﹣2an﹣1=an

∴an=2an﹣1，從而可得數列{an}是等比數列

∴an=a12n﹣1= =

綜上可得，當a1=0時，an=0，當a1≠0時，

（2）解：當a1＞0且λ=100時，令

由（1）可知

∴{bn}是單調遞減的等差數列，公差為﹣lg2

∴b1＞b2＞…＞b6= ＞0

當n≥7時，

∴數列 的前6項和最大

【解析】（1）由題意，n=1時，由已知可知a1（λa1﹣2）=0，分類討論：由a1=0，及a1≠0，結合數列的和與項的遞推公式可求（2）由a1＞0且λ=100時，令 ，則 ，結合數列的單調性可求和的最大項
【考點精析】掌握數列的前n項和和數列的通項公式是解答本題的根本，需要知道數列{an}的前n項和sn與通項an的關系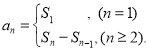；如果數列an的第n項與n之間的關系可以用一個公式表示，那么這個公式就叫這個數列的通項公式．