
【題目】【2018四川南充市高三第二次(3月)高考適應性考試】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(I)求橢圓![]() 的方程;
的方程;
(II)直線![]() 平行于
平行于![]() 為坐標原點),且與橢圓
為坐標原點),且與橢圓![]() 交于
交于![]() 兩個不同的點,若
兩個不同的點,若![]() 為鈍角,求直線
為鈍角,求直線![]() 在
在![]() 軸上的截距
軸上的截距![]() 的取值范圍.
的取值范圍.
 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案科目:高中數學 來源: 題型:
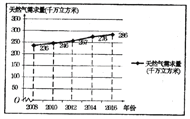
【題目】2017年12月,針對國內天然氣供應緊張的問題,某市政府及時安排部署,加氣站采取了緊急限氣措施,全市居民打響了節約能源的攻堅戰.某研究人員為了了解天然氣的需求狀況,對該地區某些年份天然氣需求量進行了統計,并繪制了相應的折線圖.
(Ⅰ)由折線圖可以看出,可用線性回歸模型擬合年度天然氣需示量![]() (單位:千萬立方米)與年份
(單位:千萬立方米)與年份![]() (單位:年)之間的關系.并且已知
(單位:年)之間的關系.并且已知![]() 關于
關于![]() 的線性回歸方程是
的線性回歸方程是![]() ,試確定
,試確定![]() 的值,并預測2018年該地區的天然氣需求量;
的值,并預測2018年該地區的天然氣需求量;
(Ⅱ)政府部門為節約能源出臺了《購置新能源汽車補貼方案》,該方案對新能源汽車的續航里程做出了嚴格規定,根據續航里程的不同,將補貼金額劃分為三類,A類:每車補貼1萬元,B類:每車補貼2.5萬元,C類:每車補貼3.4萬元.某出租車公司對該公司60輛新能源汽車的補貼情況進行了統計,結果如下表:
類型 |
|
|
|
車輛數目 | 10 | 20 | 30 |
為了制定更合理的補貼方案,政府部門決定利用分層抽樣的方式了解出租車公司新能源汽車的補貼情況,在該出租車公司的60輛車中抽取6輛車作為樣本,再從6輛車中抽取2輛車進一步跟蹤調查.若抽取的2輛車享受的補貼金額之和記為“![]() ”,求
”,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】傳承傳統文化再掀熱潮,央視科教頻道以詩詞知識競賽為主的《中國詩詞大會》火爆熒屏.將中學組和大學組的參賽選手按成績分為優秀、良好、一般三個等級,隨機從中抽取了100名選手進行調查,下面是根據調查結果繪制的選手等級人數的條形圖.

(1)若將一般等級和良好等級合稱為合格等級,根據已知條件完成下面的![]() 列聯表,據此資料你是否有95%的把握認為選手成績“優秀”與文化程度有關?
列聯表,據此資料你是否有95%的把握認為選手成績“優秀”與文化程度有關?
優秀 | 合格 | 合計 | |
大學組 | |||
中學組 | |||
合計 |
注:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.005 |
| 2.706 | 3.841 | 7.879 |
(2)若參賽選手共6萬人,用頻率估計概率,試估計其中優秀等級的選手人數.
(3)在優秀等級的選手中取6名,依次編號為1,2,3,4,5,6.在良好等級的選手中取6名,依次編號為1,2,3,4,5,6,在選出的6名優秀等級的選手中任取一名,記其編號為![]()
![]() ,求使得方程組
,求使得方程組![]() 有唯一一組實數解
有唯一一組實數解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點,離心率為
的中心在原點,離心率為![]() ,右焦點到直線
,右焦點到直線![]() 的距離為2.
的距離為2.
(1)求橢圓![]() 的方程;
的方程;
(2)橢圓下頂點為![]() ,直線
,直線![]() (
(![]() )與橢圓相交于不同的兩點
)與橢圓相交于不同的兩點![]() ,當
,當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某班的50名學生進行不記名問卷調查,內容為本周使用手機的時間長,如表:
時間長(小時) |
|
|
|
|
|
女生人數 | 4 | 11 | 3 | 2 | 0 |
男生人數 | 3 | 17 | 6 | 3 | 1 |
(1)求這50名學生本周使用手機的平均時間長;
(2)時間長為![]() 的7名同學中,從中抽取兩名,求其中恰有一個女生的概率;
的7名同學中,從中抽取兩名,求其中恰有一個女生的概率;
(3)若時間長為![]() 被認定“不依賴手機”,
被認定“不依賴手機”,![]() 被認定“依賴手機”,根據以上數據完成
被認定“依賴手機”,根據以上數據完成![]() 列聯表:
列聯表:
不依賴手機 | 依賴手機 | 總計 | |
女生 | |||
男生 | |||
總計 |
能否在犯錯概率不超過0.15的前提下,認為學生的性別與依賴手機有關系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)若曲線![]() 與曲線
與曲線![]() 在公共點處有共同的切線,求實數
在公共點處有共同的切線,求實數![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,試問函數![]() 是否有零點?如果有,求出該零點;若沒有,請說明理由.
是否有零點?如果有,求出該零點;若沒有,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某石化集團獲得了某地深海油田區塊的開采權.集團在該地區隨機初步勘探了部分幾口井.取得了地質資料,進入全面勘探時期后.集團按網絡點來布置井位進行全面勘探.由于勘探一口井的費用很高.如果新設計的井位與原有井位重合或接近.便利用舊并的地質資料.不必打這日新并,以節約勘探費與用,勘探初期數據資料見如表:
井號 |
|
|
|
|
|
|
坐標 |
|
|
|
|
|
|
鉆探深度 |
|
|
|
|
|
|
出油量 |
|
|
|
|
|
|
(參考公式和計算結果: ,
,![]() ,
,![]() ,
,![]() ).
).
(![]() )
)![]() 號舊井位置線性分布,借助前
號舊井位置線性分布,借助前![]() 組數據求得回歸直線方程為
組數據求得回歸直線方程為![]() ,求
,求![]() 的值.
的值.
(![]() )現準備勘探新井
)現準備勘探新井![]() ,若通過
,若通過![]() ,
,![]() ,
,![]() ,
,![]() 號井計算出的
號井計算出的![]() ,
,![]() 的值(
的值(![]() ,
,![]() 精確到
精確到![]() )相比于(
)相比于(![]() )中的
)中的![]() ,
,![]() ,值之差不超過
,值之差不超過![]() .則使用位置最接近的已有舊井
.則使用位置最接近的已有舊井![]() .否則在新位置打開,請判斷可否使用舊井?
.否則在新位置打開,請判斷可否使用舊井?
(![]() )設出油量與勘探深度的比值
)設出油量與勘探深度的比值![]() 不低于
不低于![]() 的勘探井稱為優質井,那么在原有
的勘探井稱為優質井,那么在原有![]() 口井中任意勘探
口井中任意勘探![]() 口井,求勘探優質井數
口井,求勘探優質井數![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com