【題目】某區(qū)工商局、消費者協(xié)會在
月
號舉行了以“攜手共治，暢享消費”為主題的大型宣傳咨詢服務(wù)活動，著力提升消費者維權(quán)意識．組織方從參加活動的群眾中隨機抽取
名群眾，按他們的年齡分組：第
組
，第
組
，第組
，第
組
，第
組
，得到的頻率分布直方圖如圖所示.
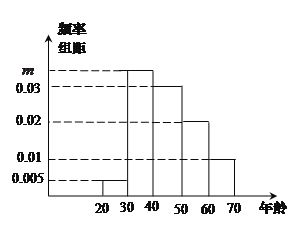
（Ⅰ）若電視臺記者要從抽取的群眾中選人進行采訪，求被采訪人恰好在第組或第組的概率；
（Ⅱ）已知第組群眾中男性有人，組織方要從第組中隨機抽取名群眾組成維權(quán)志愿者服務(wù)隊，求至少有兩名女性的概率.
閱讀快車系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】某單位為了解其后勤部門的服務(wù)情況，隨機訪問了40名其他部門的員工，根據(jù)這40名員工對后勤部門的評分情況，繪制了頻率分布直方圖如圖所示，其中樣本數(shù)據(jù)分組區(qū)間為
，
，
，
，
，
.
（1）求
的值；
（2）估計該單位其他部門的員工對后勤部門的評分的中位數(shù)；
（3）以評分在
的受訪者中，隨機抽取2人，求此2人中至少有1人對后勤部門評分在內(nèi)的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】《周髀算經(jīng)》 是我國古代的天文學(xué)和數(shù)學(xué)著作。其中一個問題的大意為：一年有二十四個節(jié)氣（如圖），每個節(jié)氣晷長損益相同（即物體在太陽的照射下影子長度的增加量和減少量相同）．若冬至晷長一丈三尺五寸，夏至晷長一尺五寸（注：ー丈等于十尺，一尺等于十寸），則立冬節(jié)氣的晷長為（ ）
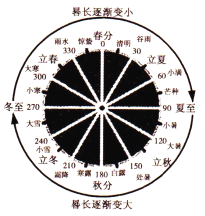
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)
，
或
，
，
．
從以下兩個命題中任選一個進行證明：
當(dāng)
時函數(shù)
恰有一個零點；
當(dāng)
時函數(shù)
恰有一個零點；
如圖所示當(dāng)
時
如
，
與
的圖象“好像”只有一個交點，但實際上這兩個函數(shù)有兩個交點，請證明：當(dāng)時，與兩個交點．
若方程
恰有4個實數(shù)根，請結(jié)合
的研究，指出實數(shù)k的取值范圍不用證明
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，若在其定義域內(nèi)存在實數(shù)
滿足
，則稱函數(shù)為“局部奇函數(shù)”，若函數(shù)
是定義在
上的“局部奇函數(shù)”，則實數(shù)
的取值范圍是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】恩施州某電影院共有1000個座位，票價不分等次，根據(jù)電影院的經(jīng)營經(jīng)驗，當(dāng)每張票價不超過10元時、票可全部售出；當(dāng)票價高于10元時，每提高1元，將有30張票不能售出，為了獲得更好的收入，需要給電影院一個合適的票價，基本條件是：①為了方便找零和算賬，票價定為1元的整數(shù)倍．②影院放映一場電影的成本是4000元，票房收入必須高于成本，用x（元）表示每張票價，用y（元）表示該電影放映一場的純收入（除去成本后的收入）．
（1）求函數(shù)y＝f（x）的解析式；
（2）票價定為多少時，電影放映一場的純收入最大？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（ x R ,且 e 為自然對數(shù)的底數(shù)）．
⑴ 判斷函數(shù) f x 的單調(diào)性與奇偶性；
⑵是否存在實數(shù) t ，使不等式
對一切的 x R 都成立？若存在，求出 t 的值，若 不存在說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在
平面上有一點列
、
、
、
、，對每個正整數(shù)
，點
位于函數(shù)
的圖像上，且點、點
與點
構(gòu)成一個以為頂角頂點的等腰三角形；
（1）求點的縱坐標(biāo)
的表達式；
（2）若對每個自然數(shù)，以、
、
為邊長能構(gòu)成一個三角形，求
的取值范圍；
（3）設(shè)
，若取（2）中確定的范圍內(nèi)的最小整數(shù)，問數(shù)列
的最大項的項數(shù)是多少？試說明理由；
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
（1）求函數(shù)
的解析式；
（2）設(shè)
，是否存在實數(shù)a，使得當(dāng)
時，恒有
成立，若存在，求出a的取值范圍；若不存在，說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
