【題目】已知圓
，直線
，
（1）求證：直線
恒過定點；
（2）判斷直線被圓
截得的弦長何時最長，何時最短?并求截得的弦長最短時，求
的值以及最短長度.
科目：高中數學 來源： 題型：
【題目】中學為研究學生的身體素質與體育鍛煉時間的關系，對該校200名高三學生平均每天體育鍛煉時間進行調查，如表：（平均每天鍛煉的時間單位：分鐘）
平均每天鍛煉的時間/分鐘 |
|
|
|
|
|
|
總人數 | 20 | 36 | 44 | 50 | 40 | 10 |
將學生日均體育鍛煉時間在
的學生評價為“鍛煉達標”.
（1）請根據上述表格中的統計數據填寫下面的
列聯表；
鍛煉不達標 | 鍛煉達標 | 合計 | |
男 | |||
女 | 20 | 110 | |
合計 |
并通過計算判斷，是否能在犯錯誤的概率不超過0.025的前提下認為“鍛煉達標”與性別有關？
（2）在“鍛煉達標”的學生中，按男女用分層抽樣方法抽出10人，進行體育鍛煉體會交流，
（i）求這10人中，男生、女生各有多少人？
（ii）從參加體會交流的10人中，隨機選出2人作重點發言，記這2人中女生的人數為
，求的分布列和數學期望.
參考公式：
，其中
.
臨界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
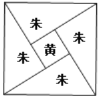
【題目】三國時期吳國數學家趙爽所注《周牌算經》中給出了勾股定理的絕妙證明.右面是趙爽的弦圖及注文，弦圖是一個以勾股形之弦為邊的正方形，其面積稱為弦實，圖中包含四個全等的勾股形及一個小正方形，分別涂成紅（朱）色及黃色，其面積稱為朱實黃實，利用
勾
股
（股
勾）
朱實
黃實
弦實，化簡，得勾
股
弦
，設勾股中勾股比為
，若向弦圖內隨機拋擲
顆圖釘（大小忽略不計），則落在黃色圖形內的圖釘顆數大約為（ ）（參考數據
，
）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線過點(3，－2)且與橢圓4x2＋9y2＝36有相同的焦點．
(1)求雙曲線的標準方程；
(2)若點M在雙曲線上，F1，F2為左、右焦點，且|MF1|＋|MF2|＝6
，試判別△MF1F2的形狀．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數方程為
（
為參數）.以坐標原點
為原點，
軸正半軸為極軸建立極坐標系，直線
的極坐標方程為
.
（1）求曲線的普通方程和直線的直角坐標方程；
（2）設直線與軸的交點為
，過點作傾斜角為
的直線
與曲線交于
兩點，求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】黃河被稱為我國的母親河，它的得名據說來自于河水的顏色，黃河因攜帶大量泥沙所以河水呈現黃色， 黃河的水源來自青海高原，上游的1000公里的河水是非常清澈的.只是中游流經黃土高原，又有太多攜帶有大量泥沙的河流匯入才造成黃河的河水逐漸變得渾濁.在劉家峽水庫附近，清澈的黃河和攜帶大量泥沙的洮河匯合，在兩條河流的交匯處，水的顏色一清一濁，互不交融，涇渭分明，形成了一條奇特的水中分界線，設黃河和洮河在汛期的水流量均為2000
，黃河水的含沙量為
，洮河水的含沙量為
，假設從交匯處開始沿岸設有若干個觀測點，兩股河水在流經相鄰的觀測點的過程中，其混合效果相當于兩股河水在1秒內交換
的水量，即從洮河流入黃河的水混合后，又從黃河流入的水到洮河再混合.
（1）求經過第二個觀測點時，兩股河水的含沙量；
（2）從第幾個觀測點開始，兩股河水的含沙量之差小于
?（不考慮泥沙沉淀）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】AB是圓O的直徑，點C是圓O上異于AB的動點，過動點C的直線VC垂直于圓O所在平面，D，E分別是VA，VC的中點.
（1）判斷直線DE與平面VBC的位置關系，并說明理由；
（2）當△VAB為邊長為
的正三角形時，求四面體V﹣DEB的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
