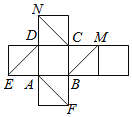
【題目】如圖是正方體的平面展開圖，在這個正方體中，有以下四個命題:①
平面ADNE；②
平面ABFE；③平面
平面AFN；④平面
平面NCF.其中正確命題的序號是( )
A.②③B.①②③C.②③④D.①②③④
【答案】A
【解析】
把正方體的平面展開圖還原成正方體ABCDEFMN，得出BM∥平面ADNE，判斷①錯誤；
由平面DCMN∥平面ABFE，得出CN∥平面ABFE，判斷②正確；
由BD∥FN，得出BD∥平面AFN，同理BM∥平面AFN，證明平面BDM∥平面AFN，判斷③正確；
由BD∥FN，BE∥CN，且BD∩BE＝B，證明平面BDE∥平面NCF，判斷④錯誤.
解：把正方體的平面展開圖還原成正方體ABCD﹣EFMN，如圖1所示；
對于①，平面BCMF∥平面ADNE，BM平面BCMF，
∴BM∥平面ADNE，①錯誤；
對于②，平面DCMN∥平面ABFE，CN平面DCMN，
∴CN∥平面ABFE，②正確；
對于③，如圖2所示，
BD∥FN，BD平面AFN，FN平面AFN，
∴BD∥平面AFN；
同理BM∥平面AFN，且BD∩BM＝B，
∴平面BDM∥平面AFN，③正確；
對于④，如圖3所示，同③可得平面BDE∥平面NCF，④錯誤.
綜上，正確的命題序號是②③.
故選：A.
科目：高中數學 來源： 題型：
【題目】研究變量
，
得到一組樣本數據，進行回歸分析，有以下結論
①殘差平方和越小的模型，擬合的效果越好；
②用相關指數
來刻畫回歸效果，越小說明擬合效果越好；
③線性回歸方程對應的直線
至少經過其樣本數據點中的一個點；
④若變量和之間的相關系數為
，則變量和之間的負相關很強.
以上正確說法的個數是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，且橢圓上一點與橢圓的兩個焦點構成的三角形周長為
．
（Ⅰ）求橢圓
的方程；
（Ⅱ）設直線
與橢圓交于
，
兩點，且以
為直徑的圓過橢圓的右頂點
，求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，有一矩形鋼板ABCD缺損了一角(如圖所示)，邊緣線OM上每一點到點D的距離都等于它到邊AB的距離．工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形，若AB＝1m，AD＝0.5m，則五邊形ABCEF的面積最大值為____m2.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了推行“智慧課堂”教學，某老師分別用傳統教學和“智慧課堂”兩種不同的教學方式，在甲、乙兩個平行班級進行教學實驗，為了比較教學效果，期屮考試后，分別從兩個班級屮各隨機抽取20名學生的成績進行統計，結果如下表：記成績不低于70分者為“成績優良”.
分數 |
|
|
|
|
|
甲班頻數 | 5 | 6 | 4 | 4 | 1 |
乙班頻數 | 1 | 3 | 6 | 5 | 5 |
（1）由以上統計數據填寫下面
列聯表，并判斷“成績優良與教學方式是否有關”?
甲班 | 乙班 | 總計 | |
成績優良 | |||
| p>成績不優良 | |||
總計 |
附：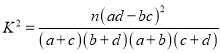 
.
臨界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
（2）現從上述40人中，學校按成績是否優良采川分層扣樣的方法扣取8人進行考核.在這8人中,記成績不優良的乙班人數為
，求
的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
(其中
， 
).
（1）當
時，若
在其定義域內為單調函數，求
的取值范圍；
（2）當
時，是否存在實數
，使得當
時，不等式
恒成立，如果存在，求
的取值范圍，如果不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖：已知四棱錐P—ABCD的底面ABCD是平行四邊形，PA⊥面ABCD，M是AD的中點，N是PC的中點.
（1）求證：MN∥面PAB；
（2）若平面PMC⊥面PAD，求證：CM⊥AD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
