
【題目】如圖,四棱錐![]() 的側(cè)面
的側(cè)面![]() 是正三角形,
是正三角形,![]() ,且
,且![]() ,
,![]() ,
,![]() 是
是![]() 中點(diǎn).
中點(diǎn).
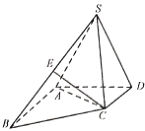
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]()
【解析】
(1) 取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,再證明四邊形
,再證明四邊形![]() 是平行四邊形即可.
是平行四邊形即可.
(2) 取![]() 中點(diǎn)
中點(diǎn)![]() ,連接
,連接![]() ,
,![]() ,根據(jù)線面垂直性質(zhì)計(jì)算可得
,根據(jù)線面垂直性質(zhì)計(jì)算可得![]() ,再以
,再以![]() 為原點(diǎn),建立空間直角坐標(biāo)系,利用空間向量的方法求解二面角
為原點(diǎn),建立空間直角坐標(biāo)系,利用空間向量的方法求解二面角![]() 的余弦值即可.
的余弦值即可.
(1)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,
,

因?yàn)?/span>![]() 是
是![]() 中點(diǎn),
中點(diǎn),
所以![]() ,且
,且![]() ,
,
又因?yàn)?/span>![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
即四邊形![]() 是平行四邊形,
是平行四邊形,
所以![]() ,
,
又因?yàn)?/span>![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)方法一:取![]() 中點(diǎn)
中點(diǎn)![]() ,連接
,連接![]() ,
,![]() ,
,
因?yàn)?/span>![]() 是正三角形,所以
是正三角形,所以![]() ,
,
因?yàn)槠矫?/span>![]() 平面
平面![]() ,
,![]()
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,
,
故![]() ,
,
以![]() 為原點(diǎn),建立如圖所示的空間直角坐標(biāo)系
為原點(diǎn),建立如圖所示的空間直角坐標(biāo)系![]() ,則
,則![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,
,![]() ,
,
令![]() 得
得![]() ,
,
易知平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.
方法二:過![]() 作
作![]() 交
交![]() 于
于![]() ,
,
所以![]() ,且
,且![]() 平面
平面![]() ,
,
過![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,
,
所以![]() ,
,
所以![]() 為二面角
為二面角![]() 的平面角,
的平面角,
因?yàn)?/span>![]() ,
,![]() ,
,
因?yàn)?/span>![]() 平面
平面![]() ,
,
所以![]() ,且
,且![]() ,
,
又因?yàn)?/span>![]() ,所以
,所以![]() ,
,![]() ,
,
故![]() ,所以二面角
,所以二面角![]() 的余弦值為
的余弦值為![]() .
.




| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】按照水果市場(chǎng)的需要等因素,水果種植戶把某種成熟后的水果按其直徑![]() 的大小分為不同等級(jí).某商家計(jì)劃從該種植戶那里購進(jìn)一批這種水果銷售.為了了解這種水果的質(zhì)量等級(jí)情況,現(xiàn)隨機(jī)抽取了100個(gè)這種水果,統(tǒng)計(jì)得到如下直徑分布表(單位:mm):
的大小分為不同等級(jí).某商家計(jì)劃從該種植戶那里購進(jìn)一批這種水果銷售.為了了解這種水果的質(zhì)量等級(jí)情況,現(xiàn)隨機(jī)抽取了100個(gè)這種水果,統(tǒng)計(jì)得到如下直徑分布表(單位:mm):
d |
|
|
|
|
|
等級(jí) | 三級(jí)品 | 二級(jí)品 | 一級(jí)品 | 特級(jí)品 | 特級(jí)品 |
頻數(shù) | 1 | m | 29 | n | 7 |
用分層抽樣的方法從其中的一級(jí)品和特級(jí)品共抽取6個(gè),其中一級(jí)品2個(gè).
(1)估計(jì)這批水果中特級(jí)品的比例;
(2)已知樣本中這批水果不按等級(jí)混裝的話20個(gè)約1斤,該種植戶有20000斤這種水果待售,商家提出兩種收購方案:
方案A:以6.5元/斤收購;
方案B:以級(jí)別分裝收購,每袋20個(gè),特級(jí)品8元/袋,一級(jí)品5元/袋,二級(jí)品4元/袋,三級(jí)品3元/袋.
用樣本的頻率分布估計(jì)總體分布,問哪個(gè)方案種植戶的收益更高?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】武漢市掀起了轟轟烈烈的“十日大會(huì)戰(zhàn)”,要在10天之內(nèi),對(duì)武漢市民做一次全員檢測(cè),徹底摸清武漢市的詳細(xì)情況.某醫(yī)院為篩查冠狀病毒,需要檢驗(yàn)血液是否為陽性,現(xiàn)有![]() 份血液樣本,有以下兩種檢驗(yàn)方式:
份血液樣本,有以下兩種檢驗(yàn)方式:
方案①:將每個(gè)人的血分別化驗(yàn),這時(shí)需要驗(yàn)1000次.
方案②:按![]() 個(gè)人一組進(jìn)行隨機(jī)分組,把從每組
個(gè)人一組進(jìn)行隨機(jī)分組,把從每組![]() 個(gè)人抽來的血混合在一起進(jìn)行檢驗(yàn),如果每個(gè)人的血均為陰性,則驗(yàn)出的結(jié)果呈陰性,這
個(gè)人抽來的血混合在一起進(jìn)行檢驗(yàn),如果每個(gè)人的血均為陰性,則驗(yàn)出的結(jié)果呈陰性,這![]() 個(gè)人的血就只需檢驗(yàn)一次(這時(shí)認(rèn)為每個(gè)人的血化驗(yàn)
個(gè)人的血就只需檢驗(yàn)一次(這時(shí)認(rèn)為每個(gè)人的血化驗(yàn)![]() 次);否則,若呈陽性,則需對(duì)這
次);否則,若呈陽性,則需對(duì)這![]() 個(gè)人的血樣再分別進(jìn)行一次化驗(yàn)這樣,該組
個(gè)人的血樣再分別進(jìn)行一次化驗(yàn)這樣,該組![]() 個(gè)人的血總共需要化驗(yàn)
個(gè)人的血總共需要化驗(yàn)![]() 次. 假設(shè)此次檢驗(yàn)中每個(gè)人的血樣化驗(yàn)呈陽性的概率為
次. 假設(shè)此次檢驗(yàn)中每個(gè)人的血樣化驗(yàn)呈陽性的概率為![]() ,且這些人之間的試驗(yàn)反應(yīng)相互獨(dú)立.
,且這些人之間的試驗(yàn)反應(yīng)相互獨(dú)立.
(1)設(shè)方案②中,某組![]() 個(gè)人中每個(gè)人的血化驗(yàn)次數(shù)為
個(gè)人中每個(gè)人的血化驗(yàn)次數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(2)設(shè)![]() . 試比較方案②中,
. 試比較方案②中,![]() 分別取2,3,4時(shí),各需化驗(yàn)的平均總次數(shù);并指出在這三種分組情況下,相比方案①,化驗(yàn)次數(shù)最多可以減少多少次?(最后結(jié)果四舍五入保留整數(shù))
分別取2,3,4時(shí),各需化驗(yàn)的平均總次數(shù);并指出在這三種分組情況下,相比方案①,化驗(yàn)次數(shù)最多可以減少多少次?(最后結(jié)果四舍五入保留整數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(在花卉進(jìn)行硬枝扦插過程中,常需要用生根粉調(diào)節(jié)植物根系生長(zhǎng).現(xiàn)有20株使用了生根粉的花卉,在對(duì)最終“花卉存活”和“花卉死亡”進(jìn)行統(tǒng)計(jì)的同時(shí),也對(duì)在使用生根粉2個(gè)小時(shí)后的生根量進(jìn)行了統(tǒng)計(jì),這20株花卉生根量如下表所示,其中生根量在6根以下的視為“不足量”,大于等于6根為“足量”.現(xiàn)對(duì)該20株花卉樣本進(jìn)行統(tǒng)計(jì),其中“花卉存活”的13株.已知“花卉存活”但生根量“不足量”的植株共1株.
編號(hào) | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
生根量 | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 9 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成![]() 列聯(lián)表,并判斷是否可以在犯錯(cuò)誤概率不超過1%的前提下,認(rèn)為“花卉的存活”與“生根足量”有關(guān)?
列聯(lián)表,并判斷是否可以在犯錯(cuò)誤概率不超過1%的前提下,認(rèn)為“花卉的存活”與“生根足量”有關(guān)?
生根足量 | 生根不足量 | 總計(jì) | |
花卉存活 | |||
花卉死亡 | |||
總計(jì) | 20 |
(2)若在該樣本“生根不足量”的植株中隨機(jī)抽取3株,求這3株中恰有1株“花卉存活”的概率.
參考數(shù)據(jù):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
獨(dú)立性檢驗(yàn)中的 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() 的右頂點(diǎn)為A,左焦點(diǎn)為
的右頂點(diǎn)為A,左焦點(diǎn)為![]() ,過點(diǎn)A的直線
,過點(diǎn)A的直線![]() 與橢圓C的另一個(gè)交點(diǎn)為B,
與橢圓C的另一個(gè)交點(diǎn)為B,![]() 軸,點(diǎn)
軸,點(diǎn)![]()
![]() 在直線
在直線![]() 上.
上.
(I)求![]() 的面積;
的面積;
(II)過點(diǎn)S的直線![]() 與橢圓C交于P,Q兩點(diǎn),且
與橢圓C交于P,Q兩點(diǎn),且![]() 的面積是
的面積是![]() 的面積的6倍,求直線
的面積的6倍,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() ,過點(diǎn)
,過點(diǎn)![]() 作互相垂直的兩條直線分別交橢圓
作互相垂直的兩條直線分別交橢圓![]() 于點(diǎn)
于點(diǎn)![]() (
(![]() 與
與![]() 不重合).
不重合).
(1)證明:直線![]() 過定點(diǎn)
過定點(diǎn)![]() ;
;
(2)若以點(diǎn)![]() 為圓心的圓與直線
為圓心的圓與直線![]() 相切,且切點(diǎn)為線段
相切,且切點(diǎn)為線段![]() 的中點(diǎn),求四邊形
的中點(diǎn),求四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值為0.
的最小值為0.
(1)若![]() 的極大值為
的極大值為![]() ,求
,求![]() 的單調(diào)減區(qū)間;
的單調(diào)減區(qū)間;
(2)若![]() ,
,![]() 的是
的是![]() 的兩個(gè)極值點(diǎn),且
的兩個(gè)極值點(diǎn),且![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
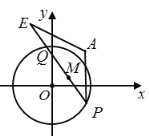
【題目】已知圓![]() 點(diǎn)
點(diǎn)![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 在直線
在直線![]() 上且滿足
上且滿足![]() .若
.若![]() ,則弦
,則弦![]() 中點(diǎn)
中點(diǎn)![]() 的橫坐標(biāo)的取值范圍為_____________.
的橫坐標(biāo)的取值范圍為_____________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com