
���}Ŀ����֪����(sh��)![]() .
.
��1��������![]() ���c(di��n)
���c(di��n)![]() ̎���о����̞�
̎���о����̞�![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ֵ��
��ֵ��
��2��������(sh��)![]() ���ڃɂ�(g��)���c(di��n)����(sh��)��(sh��)
���ڃɂ�(g��)���c(di��n)����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
���𰸡���1��![]() ����2��
����2��![]()
��������
��1��ֱ�Ӹ���(j��)���c(di��n)̎�Č�(d��o)��(sh��)ֵ�����о���б����⣻
��2��׃�Ξ鷽��![]() �Ѓɂ�(g��)��(sh��)��(sh��)�����D(zhu��n)����ֱ��
�Ѓɂ�(g��)��(sh��)��(sh��)�����D(zhu��n)����ֱ��![]() �c����(sh��)
�c����(sh��)![]() �ĈD���Ѓɂ�(g��)���c(di��n)����������(sh��)
�ĈD���Ѓɂ�(g��)���c(di��n)����������(sh��)![]() �ĈD�Ķ���⣮
�ĈD�Ķ���⣮
�⣺��1����?y��n)?/span>![]() ��
��
��![]()
����![]() .
.
��?y��n)��������c(di��n)![]() ̎���о����̞�
̎���о����̞�![]() ��
��
����![]() ��
��
��![]() ��
��
��2��![]() ���ڃɂ�(g��)���c(di��n)��
���ڃɂ�(g��)���c(di��n)��
������![]() �Ѓɂ�(g��)����
�Ѓɂ�(g��)����
Ҳ��ֱ��![]() �c����(sh��)
�c����(sh��)![]() �ĈD���Ѓɂ�(g��)���c(di��n)��
�ĈD���Ѓɂ�(g��)���c(di��n)��
ӛ![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() �φ��{(di��o)�f�p����
�φ��{(di��o)�f�p����![]() �φ��{(di��o)�f������
�φ��{(di��o)�f������![]() �φ��{(di��o)�f�p��
�φ��{(di��o)�f�p��
��![]() ��
��![]() �r(sh��)
�r(sh��)![]() ��
��
��ֱ��![]() �^(gu��)
�^(gu��)![]() ��б�ʞ�
��б�ʞ�![]() ��
��
���®�(hu��)��![]() �D�����D�����^��D��֪��
�D�����D�����^��D��֪��
��(d��ng)![]() �r(sh��)��ֱ��
�r(sh��)��ֱ��![]() �c
�c![]() �ĈD����Ѓɂ�(g��)���c(di��n)��
�ĈD����Ѓɂ�(g��)���c(di��n)��
��(d��ng)![]() �r(sh��)ֱ��
�r(sh��)ֱ��![]() �c
�c![]() �ĈD��ֻ��һ��(g��)���c(di��n)��
�ĈD��ֻ��һ��(g��)���c(di��n)��
�C�ϣ�����(sh��)![]() ���ڃɂ�(g��)���c(di��n)����(sh��)��(sh��)
���ڃɂ�(g��)���c(di��n)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������![]() .
.
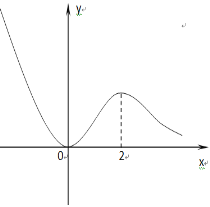


 ��x��܇(ch��)ϵ�д�
��x��܇(ch��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��.
��.
����������(sh��)![]() ��ӑՓ
��ӑՓ![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
����������(sh��)![]() ��(d��o)��(sh��)
�Č�(d��o)��(sh��)![]() �ăɂ�(g��)���c(di��n)��С�������Ξ�
�ăɂ�(g��)���c(di��n)��С�������Ξ�![]() ��
��![]() ���C����
���C����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У���֪����
�У���֪����![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�������S��O�S�������O����(bi��o)ϵ��ֱ��
�S�������S��O�S�������O����(bi��o)ϵ��ֱ��![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1��������![]() ����ͨ���̺�ֱ��
����ͨ���̺�ֱ��![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2�����侀![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��![]() ��.�O(sh��)
��.�O(sh��)![]() �c
�c![]() �ཻ���c(di��n)
�ཻ���c(di��n)![]() ��
��![]() �c
�c![]() �ཻ���c(di��n)
�ཻ���c(di��n)![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���̴�λ������������(sh��)�W(xu��)�ң����ġ��¾�ֱָ�㷨�y(t��ng)�ڡ����Ї�(gu��)�vʷ��һ��Ӱ푾�������������е�33��(w��n)�����������ǹ�һ�⣬���ÿ���߂�(g��)����(w��n)ԓ���ɣ�����D�ǽ�Qԓ��(w��n)�}�ij����D����(zh��)��ԓ�����D�����ԓ����ӵĿ���(sh��)S�飨 ��
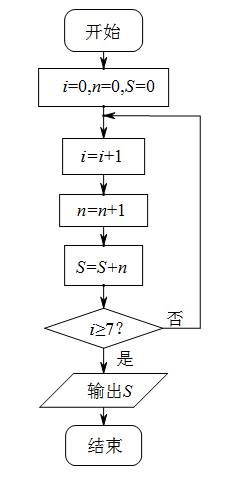
A.28B.56C.84D.120
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
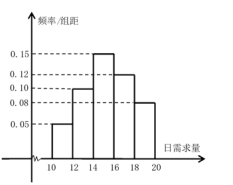
���}Ŀ��������ij�̵��N(xi��o)��ij���r����(j��ng)���y(t��ng)Ӌ(j��)�˴���(ji��)ǰ��50��ԓ���r����������![]() ��
��![]() ����λ����������l�ʷֲ�ֱ���D���D��ʾ.ԓ���rÿ���M(j��n)؛1�Σ�ÿ�N(xi��o)��1����ɫ@��40Ԫ������������ʣ��ĺ��r���r(ji��)̎�������r(ji��)̎���ĺ��rÿ����̝�p10Ԫ����������(y��ng)�ɏ������̵��{(di��o)�ܣ��{(di��o)�ܵĺ��r�N(xi��o)��1����ɫ@��30Ԫ.���O(sh��)�̵�ԓ���rÿ����M(j��n)؛����14����̵��N(xi��o)��ԓ���r��������(r��n)��
����λ����������l�ʷֲ�ֱ���D���D��ʾ.ԓ���rÿ���M(j��n)؛1�Σ�ÿ�N(xi��o)��1����ɫ@��40Ԫ������������ʣ��ĺ��r���r(ji��)̎�������r(ji��)̎���ĺ��rÿ����̝�p10Ԫ����������(y��ng)�ɏ������̵��{(di��o)�ܣ��{(di��o)�ܵĺ��r�N(xi��o)��1����ɫ@��30Ԫ.���O(sh��)�̵�ԓ���rÿ����M(j��n)؛����14����̵��N(xi��o)��ԓ���r��������(r��n)��![]() Ԫ.
Ԫ.
��1�����̵�������(r��n)![]() �P(gu��n)����������
�P(gu��n)����������![]() �ĺ���(sh��)���_(d��)ʽ.
�ĺ���(sh��)���_(d��)ʽ.
��2������(j��)�l�ʷֲ�ֱ���D��
�ٹ�Ӌ(j��)�@50����̵�ԓ���r����������ƽ����(sh��).
�ڼ��O(sh��)���¼��l(f��)�����l�ʹ�Ӌ(j��)���ʣ�Ո(q��ng)��Ӌ(j��)������(r��n)������620Ԫ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���ڶ����w![]() �У�ƽ��
�У�ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��![]() ƽ��
ƽ��![]() ��
��![]() .
.
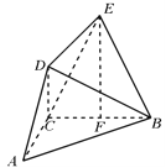
��1���C����![]() ��
��![]() ��
��![]() ��
��![]() ���c(di��n)���棻
���c(di��n)���棻
��2���������F![]() ���w�e.
���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��������![]() ���о����̞�
���о����̞�![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ֵ��
��ֵ��
��2��������(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() ���Ѓɂ�(g��)���c(di��n)����(sh��)��(sh��)
���Ѓɂ�(g��)���c(di��n)����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �����нo���Ă�(g��)�Y(ji��)Փ��
�����нo���Ă�(g��)�Y(ji��)Փ��
��![]() �����ֵ��2��
�����ֵ��2��
��![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵĆ��{(di��o)���^(q��)�g��
�ϵĆ��{(di��o)���^(q��)�g��![]() ��
��
����![]() ����
����![]() ���t
���t![]() ��
��
�܌�����![]() ����ƽ��
����ƽ��![]() ��(g��)��λ���õ�����(sh��)
��(g��)��λ���õ�����(sh��)![]() �ĈD���ٌ�����
�ĈD���ٌ�����![]()
�����c(di��n)�Ŀv����(bi��o)׃?y��u)�ԭ�?l��i)��2�����M����(bi��o)��׃�����õ�����(sh��)![]() �Č�(d��o)��(sh��)
�Č�(d��o)��(sh��)![]() �ĈD��.�������_����_______________���(xi��)�������_�Y(ji��)Փ�ľ�̖(h��o)��.
�ĈD��.�������_����_______________���(xi��)�������_�Y(ji��)Փ�ľ�̖(h��o)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij���܃x�����a(ch��n)܇(ch��)�gÿ�����a(ch��n)![]() ��(g��)������|(zh��)�z�TС��ÿ�춼��(hu��)�S�C(j��)�؏��г�ȡ50��(g��)����M(j��n)�Йz���Ƿ�ϸ����^��������ϸt�茦(du��)������������M(j��n)�Йz�飮����(j��)��������a(ch��n)��(sh��)��(j��)�ͽ�(j��ng)�(y��n)���@Щ������L(zh��ng)�ȷ������B(t��i)�ֲ�
��(g��)������|(zh��)�z�TС��ÿ�춼��(hu��)�S�C(j��)�؏��г�ȡ50��(g��)����M(j��n)�Йz���Ƿ�ϸ����^��������ϸt�茦(du��)������������M(j��n)�Йz�飮����(j��)��������a(ch��n)��(sh��)��(j��)�ͽ�(j��ng)�(y��n)���@Щ������L(zh��ng)�ȷ������B(t��i)�ֲ�![]() ����λ����
�������![]() ���������(d��)������������L(zh��ng)��
���������(d��)������������L(zh��ng)��![]() �M(m��n)��
�M(m��n)��![]() ���t�J(r��n)��ԓ����Ǻϸ�ģ���tԓ������ϸ�
���t�J(r��n)��ԓ����Ǻϸ�ģ���tԓ������ϸ�
��1�����O(sh��)ijһ��С���������ϸ�������(sh��)��![]() ����
����![]() ��
��![]() �Ĕ�(sh��)�W(xu��)����
�Ĕ�(sh��)�W(xu��)����![]() ��
��
��2��С��ij��ǡ�Ï�50��(g��)����Йz���2��(g��)���ϸ����������Դ��l�����鮔(d��ng)�����a(ch��n)����IJ��ϸ��ʣ���֪�z��һ��(g��)����ijɱ���10Ԫ����ÿ��(g��)���ϸ���������Ј�(ch��ng)����(l��i)�ēpʧ��260Ԫ�����O(sh��)![]() ��ִ���ʹ�pʧ�M��С��С���Ƿ���Ҫ�z���������������ԇ�f(shu��)�����ɣ�
��ִ���ʹ�pʧ�M��С��С���Ƿ���Ҫ�z���������������ԇ�f(shu��)�����ɣ�
�������S�C(j��)׃��![]() �������B(t��i)�ֲ�
�������B(t��i)�ֲ�![]() ���t
���t![]() ��
��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com