【題目】已知數列{an}前n項和Sn滿足：2Sn+an=1．
（1）求數列{an}的通項公式；
（2）設 
，數列{bn}的前n項和為Tn ， 求證：Tn＜2．
【答案】
（1）解：2Sn+an=1，2Sn+1+an+1=1，
∴2an+1+an+1=an，
∴3an+1=an，
又2S1+a1=1，
∴a1= 
，
∴{an}是以 為首項，以 為公比的等比數列，
∴an=（ ）n
（2）解：證明： 
= 
= 
=2（ 
﹣ 
）
∴Tn=2[（1﹣ 
）+（ ﹣ ）+…+（ ﹣ ）]=2（1﹣ ）＜2
【解析】（1）根據數列的遞推公式和對數的運算性質即可求出數列{an}的通項公式，（2）利用裂項求和即可求出數列{bn}的前n項和Tn ， 再放縮證明即可．
【考點精析】本題主要考查了數列的前n項和和數列的通項公式的相關知識點，需要掌握數列{an}的前n項和sn與通項an的關系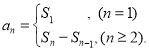
；如果數列an的第n項與n之間的關系可以用一個公式表示，那么這個公式就叫這個數列的通項公式才能正確解答此題．
科目：高中數學 來源： 題型：
【題目】已知函數 
（ 
），若函數F（x）=f（x）﹣3的所有零點依次記為x1 ， x2 ， x3 ， …，xn ， 且x1＜x2＜x3＜…＜xn ， 則x1+2x2+2x3+…+2xn﹣1+xn= ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax2﹣x﹣lnx，a∈R．
（1）當 
時，求函數f（x）的最小值；
（2）若﹣1≤a≤0，證明：函數f（x）有且只有一個零點；
（3）若函數f（x）有兩個零點，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題
函數
是
上的奇函數，命題
函數
的定義域和值域都是
，其中
.
（1）若命題
為真命題，求實數
的值；
（2）若“且
”為假命題，“或”為真命題，求實數的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的首項為1，且
，數列
滿足
，
，對任意
，都有
.
（1）求數列、的通項公式；
（2）令
，數列的前
項和為
.若對任意的，不等式
恒成立，試求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
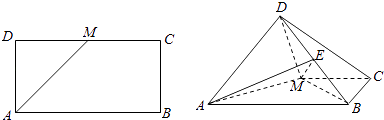
【題目】如圖，已知長方形ABCD中，AB=2 
，AD= ，M為DC的中點，將△ADM沿AM折起，使得平面ADM⊥平面ABCM （Ⅰ）求證：AD⊥BM
（Ⅱ）若點E是線段DB上的一動點，問點E在何位置時，二面角E﹣AM﹣D的余弦值為 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
，方程f2（x）+mf（x）=0（m∈R）有四個不相等的實數根，則實數m的取值范圍是（ ）
A.（﹣∞，﹣ 
）
B.（﹣ ，0）
C.（﹣ ，+∞）
D.（0， ）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場舉行有獎促銷活動，顧客購買一定金額的商品后即可參加一次抽獎.隨著抽獎活動的有效開展，參與抽獎活動的人數越來越多，該商場對前5天抽獎活動的人數進行統計，y表示第x天參加抽獎活動的人數，得到統計表如下：
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
經過進一步統計分析，發現y與x具有線性相關關系.
（1）若從這5天隨機抽取兩天，求至少有1天參加抽獎人數超過70的概率；
（2）請根據上表提供的數據，用最小二乘法求出y關于x的線性回歸方程
，并估計該活動持續7天，共有多少名顧客參加抽獎？
參考公式及數據：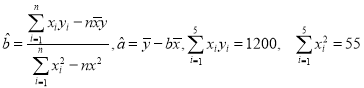
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=alnx+ 
x2﹣ax（a為常數）有兩個極值點．
（1）求實數a的取值范圍；
（2）設f（x）的兩個極值點分別為x1 ， x2 ， 若不等式f（x1）+f（x2）＜λ（x1+x2）恒成立，求λ的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com