
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的中心為坐標原點
的中心為坐標原點![]() 焦點在
焦點在![]() 軸上,右頂點
軸上,右頂點![]() 到右焦點的距離與它到右準線的距離之比為
到右焦點的距離與它到右準線的距離之比為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 是橢圓
是橢圓![]() 上關(guān)于
上關(guān)于![]() 軸對稱的任意兩點,設
軸對稱的任意兩點,設![]() ,連接
,連接![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() .求證:直線
.求證:直線![]() 過定點
過定點![]() 并求出點
并求出點![]() 的坐標;
的坐標;
(3)在(2)的條件下,過點![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)證明詳見解析,
;(2)證明詳見解析,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據(jù)題意列出關(guān)于![]() 的等式求解即可.
的等式求解即可.
(2)先根據(jù)對稱性,直線![]() 過的定點
過的定點![]() 一定在
一定在![]() 軸上,再設直線
軸上,再設直線![]() 的方程為
的方程為![]() ,聯(lián)立直線與橢圓的方程, 進而求得
,聯(lián)立直線與橢圓的方程, 進而求得![]() 的方程,并代入
的方程,并代入![]() ,
,![]() 化簡分析即可.
化簡分析即可.
(3)先分析過點![]() 的直線
的直線![]() 斜率不存在時
斜率不存在時![]() 的值,再分析存在時,設直線
的值,再分析存在時,設直線![]() 的方程為
的方程為![]() ,聯(lián)立直線與橢圓的方程,得出韋達定理再代入
,聯(lián)立直線與橢圓的方程,得出韋達定理再代入![]() 求解出關(guān)于
求解出關(guān)于![]() 的解析式,再求解范圍即可.
的解析式,再求解范圍即可.
解:![]() 設橢圓
設橢圓![]() 的標準方程
的標準方程![]() 焦距為
焦距為![]() ,
,
由題意得,![]()
由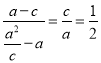 ,可得
,可得![]()
則![]() ,
,
所以橢圓![]() 的標準方程為
的標準方程為![]() ;
;
![]() 證明:根據(jù)對稱性,直線
證明:根據(jù)對稱性,直線![]() 過的定點
過的定點![]() 一定在
一定在![]() 軸上,
軸上,
由題意可知直線![]() 的斜率存在,
的斜率存在,
設直線![]() 的方程為
的方程為![]() ,
,
聯(lián)立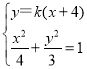 ,消去
,消去![]() 得到
得到![]() ,
,
設點![]() ,
,
則![]() .
.
所以![]() ,
,
所以![]() 的方程為
的方程為![]() ,
,
令![]() 得
得![]() ,
,
將![]() ,
,![]() 代入上式并整理,
代入上式并整理,
![]() ,
,
整理得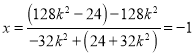 ,
,
所以,直線![]() 與
與![]() 軸相交于定點
軸相交于定點![]() .
.
![]() 當過點
當過點![]() 的直線
的直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 的方程為
的方程為![]()
![]() ,
,
此時![]() ,
,
當過點![]() 的直線
的直線![]() 斜率存在時,
斜率存在時,
設直線![]() 的方程為
的方程為![]() ,且
,且![]() 在橢圓
在橢圓![]() 上,
上,
聯(lián)立方程組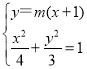 ,
,
消去![]() ,整理得
,整理得![]() ,
,
則![]() .
.
所以![]()
所以![]() ,
,
所以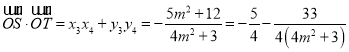 ,
,
由![]() 得
得![]() ,
,
綜上可得,![]() 的取值范圍是
的取值范圍是![]() .
.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)f(x)的單調(diào)性;
(2)若函數(shù)g(x)=f(x)﹣lnx有2個不同的極值點x1,x2(x1<x2),求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)判斷并說明函數(shù)![]() 的零點個數(shù).若函數(shù)
的零點個數(shù).若函數(shù)![]() 所有零點均在區(qū)間
所有零點均在區(qū)間![]()
![]() 內(nèi),求
內(nèi),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當![]() 時,判斷并說明函數(shù)
時,判斷并說明函數(shù)![]() 的零點個數(shù).若函數(shù)
的零點個數(shù).若函數(shù)![]() 所有零點均在區(qū)間
所有零點均在區(qū)間![]() 內(nèi),求
內(nèi),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知四棱錐![]() 的底面ABCD是邊長為2的正方形,且
的底面ABCD是邊長為2的正方形,且![]() .若四棱錐P-ABCD的五個頂點在以4為半徑的同一球面上,當PA最長時,則
.若四棱錐P-ABCD的五個頂點在以4為半徑的同一球面上,當PA最長時,則![]() ______________;四棱錐P-ABCD的體積為______________.
______________;四棱錐P-ABCD的體積為______________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 右頂點為
右頂點為![]() 過右焦點且垂直于
過右焦點且垂直于![]() 軸的直線與橢圓相交于
軸的直線與橢圓相交于![]() 兩點,所得四邊形
兩點,所得四邊形![]() 為菱形,且其面積為
為菱形,且其面積為![]() .
.
(1)求橢圓的方程;
(2)過左焦點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,試求三角形
兩點,試求三角形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】《周易》歷來被人們視作儒家群經(jīng)之首,它表現(xiàn)了古代中華民族對萬事萬物的深刻而又樸素的認識,是中華人文文化的基礎,它反映出中國古代的二進制計數(shù)的思想方法.我們用近代術(shù)語解釋為:把陽爻“- ”當作數(shù)字“1”,把陰爻“--”當作數(shù)字“0”,則八卦所代表的數(shù)表示如下:
卦名 | 符號 | 表示的二進制數(shù) | 表示的十進制數(shù) |
坤 |
| 000 | 0 |
震 |
| 001 | 1 |
坎 |
| 010 | 2 |
兌 |
| 011 | 3 |
依此類推,則六十四卦中的“屯”卦,符號“![]() ”表示的十進制數(shù)是( )
”表示的十進制數(shù)是( )
A. 18B. 17C. 16D. 15
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com