
【題目】已知![]() ,給定
,給定![]() 個(gè)整點(diǎn)
個(gè)整點(diǎn)![]() ,其中
,其中![]() .
.
(Ⅰ)當(dāng)![]() 時(shí),從上面的
時(shí),從上面的![]() 個(gè)整點(diǎn)中任取兩個(gè)不同的整點(diǎn)
個(gè)整點(diǎn)中任取兩個(gè)不同的整點(diǎn)![]() ,求
,求![]() 的所有可能值;
的所有可能值;
(Ⅱ)從上面![]() 個(gè)整點(diǎn)中任取
個(gè)整點(diǎn)中任取![]() 個(gè)不同的整點(diǎn),
個(gè)不同的整點(diǎn),![]() .
.
(i)證明:存在互不相同的四個(gè)整點(diǎn)![]() ,滿足
,滿足![]() ,
,![]() ;
;
(ii)證明:存在互不相同的四個(gè)整點(diǎn)![]() ,滿足
,滿足![]() ,
,![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)(i)詳見解析;(ii)詳見解析.
;(Ⅱ)(i)詳見解析;(ii)詳見解析.
【解析】
(Ⅰ)列出所有的整點(diǎn)后可得![]() 的所有可能值.
的所有可能值.
(Ⅱ)對于(i),可用反證法,對于(ii),可設(shè)直線![]() 上選擇了
上選擇了![]() 個(gè)的點(diǎn),計(jì)算可得諸直線上不同兩點(diǎn)的橫坐標(biāo)和的不同個(gè)數(shù)的最小值為
個(gè)的點(diǎn),計(jì)算可得諸直線上不同兩點(diǎn)的橫坐標(biāo)和的不同個(gè)數(shù)的最小值為![]() ,結(jié)合
,結(jié)合![]() 中任意不同兩項(xiàng)之和的不同的值恰有
中任意不同兩項(xiàng)之和的不同的值恰有![]() 個(gè)可得至少有一個(gè)和出現(xiàn)兩次,從而可證結(jié)論成立.
個(gè)可得至少有一個(gè)和出現(xiàn)兩次,從而可證結(jié)論成立.
解:(Ⅰ)當(dāng)![]() 時(shí),4個(gè)整點(diǎn)分別為
時(shí),4個(gè)整點(diǎn)分別為![]() .
.
所以![]() 的所有可能值
的所有可能值![]() .
.
(Ⅱ)(i)假設(shè)不存在互不相同的四個(gè)整點(diǎn)![]() ,
,
滿足![]() .
.
即在直線![]() 中至多有一條直線上取多于1個(gè)整點(diǎn),其余每條直線上至多取一個(gè)整點(diǎn), 此時(shí)符合條件的整點(diǎn)個(gè)數(shù)最多為
中至多有一條直線上取多于1個(gè)整點(diǎn),其余每條直線上至多取一個(gè)整點(diǎn), 此時(shí)符合條件的整點(diǎn)個(gè)數(shù)最多為![]() .
.
而![]() ,與已知
,與已知![]() 矛盾.
矛盾.
故存在互不相同的四個(gè)整點(diǎn)![]() ,滿足
,滿足![]() .
.
(ii)設(shè)直線![]() 上有
上有![]() 個(gè)選定的點(diǎn).
個(gè)選定的點(diǎn).
若![]() ,設(shè)
,設(shè)![]() 上的這
上的這![]() 個(gè)選定的點(diǎn)的橫坐標(biāo)為
個(gè)選定的點(diǎn)的橫坐標(biāo)為![]() ,且滿足
,且滿足![]() .
.
由![]() ,
,
知![]() 中任意不同兩項(xiàng)之和至少有
中任意不同兩項(xiàng)之和至少有![]() 個(gè)不同的值,這對于
個(gè)不同的值,這對于![]() 也成立.
也成立.
由于![]() 中任意不同兩項(xiàng)之和的不同的值恰有
中任意不同兩項(xiàng)之和的不同的值恰有![]() 個(gè),
個(gè),
而![]() ,
,
可知存在四個(gè)不同的點(diǎn)![]() ,
,
滿足![]() .
.


 優(yōu)百分課時(shí)互動系列答案
優(yōu)百分課時(shí)互動系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《孫子算經(jīng)》是中國古代重要的數(shù)學(xué)著作.其中的一道題“今有木,方三尺,高三尺,欲方五寸作枕一枚.問:得幾何?”意思是:“有一塊棱長為3尺的正方體方木,要把它作成邊長為5寸的正方體枕頭,可作多少個(gè)?”現(xiàn)有這樣的一個(gè)正方體木料,其外周已涂上油漆,則從切割后的正方體枕頭中任取一塊,恰有一面涂上油漆的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校藝術(shù)節(jié)對![]() 四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學(xué)對這四件參賽作品預(yù)測如下:
四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學(xué)對這四件參賽作品預(yù)測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”; 乙說:“
作品獲得一等獎”; 乙說:“ ![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“ ![]() 兩件作品未獲得一等獎”; 丁說:“是
兩件作品未獲得一等獎”; 丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
評獎揭曉后,發(fā)現(xiàn)這四位同學(xué)中只有兩位說的話是對的,則獲得一等獎的作品是_________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市政府為了引導(dǎo)居民合理用水,決定全面實(shí)施階梯水價(jià),居民用水原則上以住宅為單位(一套住宅為一戶).
階梯級別 | 第一階梯 | 第二階梯 | 第三階梯 |
月用水范圍(噸) |
|
|
|
為了了解全市居民月用水量的分布情況,通過抽樣,獲得了![]() 戶居民的月用水量(單位:噸),得到統(tǒng)計(jì)表如下:
戶居民的月用水量(單位:噸),得到統(tǒng)計(jì)表如下:
居民用水戶編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用水量(噸) | 7 | 8 | 8 | 9 | 10 | 11 | <>13 | 14 | 15 | 20 |
(1)若用水量不超過![]() 噸時(shí),按
噸時(shí),按![]() 元/噸計(jì)算水費(fèi);若用水量超過
元/噸計(jì)算水費(fèi);若用水量超過![]() 噸且不超過
噸且不超過![]() 噸時(shí),超過
噸時(shí),超過![]() 噸部分按
噸部分按![]() 元/噸計(jì)算水費(fèi);若用水量超過
元/噸計(jì)算水費(fèi);若用水量超過![]() 噸時(shí),超過
噸時(shí),超過![]() 噸部分按
噸部分按![]() 元/噸計(jì)算水費(fèi).試計(jì)算:若某居民用水
元/噸計(jì)算水費(fèi).試計(jì)算:若某居民用水![]() 噸,則應(yīng)交水費(fèi)多少元?
噸,則應(yīng)交水費(fèi)多少元?
(2)現(xiàn)要在這![]() 戶家庭中任意選取
戶家庭中任意選取![]() 戶,求取到第二階梯水量的戶數(shù)的分布列與期望;
戶,求取到第二階梯水量的戶數(shù)的分布列與期望;
(3)用抽到的![]() 戶家庭作為樣本估計(jì)全市的居民用水情況,從全市依次隨機(jī)抽取
戶家庭作為樣本估計(jì)全市的居民用水情況,從全市依次隨機(jī)抽取![]() 戶,若抽到
戶,若抽到![]() 戶月用水量為第一階梯的可能性最大,求
戶月用水量為第一階梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,設(shè)拋物線C1:![]() 的準(zhǔn)線1與x軸交于橢圓C2:
的準(zhǔn)線1與x軸交于橢圓C2:![]() 的右焦點(diǎn)F2,F1為C2的左焦點(diǎn).橢圓的離心率為
的右焦點(diǎn)F2,F1為C2的左焦點(diǎn).橢圓的離心率為![]() ,拋物線C1與橢圓C2交于x軸上方一點(diǎn)P,連接PF1并延長其交C1于點(diǎn)Q,M為C1上一動點(diǎn),且在P,Q之間移動.
,拋物線C1與橢圓C2交于x軸上方一點(diǎn)P,連接PF1并延長其交C1于點(diǎn)Q,M為C1上一動點(diǎn),且在P,Q之間移動.
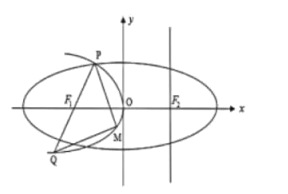
(1)當(dāng)![]() 取最小值時(shí),求C1和C2的方程;
取最小值時(shí),求C1和C2的方程;
(2)若△PF1F2的邊長恰好是三個(gè)連續(xù)的自然數(shù),當(dāng)△MPQ面積取最大值時(shí),求面積最大值以及此時(shí)直線MP的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知非零實(shí)數(shù)![]() ,
,![]() ,
,![]() 不全相等,則下列說法正確的個(gè)數(shù)是( )
不全相等,則下列說法正確的個(gè)數(shù)是( )
(1)如果![]() ,
,![]() ,
,![]() 成等差數(shù)列,則
成等差數(shù)列,則![]() ,
,![]() ,
,![]() 能構(gòu)成等差數(shù)列
能構(gòu)成等差數(shù)列
(2)如果![]() ,
,![]() ,
,![]() 成等差數(shù)列,則
成等差數(shù)列,則![]() ,
,![]() ,
,![]() 不可能構(gòu)成等比數(shù)列
不可能構(gòu)成等比數(shù)列
(3)如果![]() ,
,![]() ,
,![]() 成等比數(shù)列,則
成等比數(shù)列,則![]() ,
,![]() ,
,![]() 能構(gòu)成等比數(shù)列
能構(gòu)成等比數(shù)列
(4)如果![]() ,
,![]() ,
,![]() 成等比數(shù)列,則
成等比數(shù)列,則![]() ,
,![]() ,
,![]() 不可能構(gòu)成等差數(shù)列
不可能構(gòu)成等差數(shù)列
A.1個(gè)B.2個(gè)C.3個(gè)D.4個(gè)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是邊長為2的菱形,且
是邊長為2的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是線段
是線段![]() 上任意一點(diǎn).
上任意一點(diǎn).
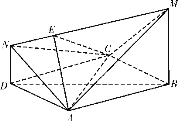
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 的最大值是
的最大值是![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù) ,下列判斷正確的是( )
,下列判斷正確的是( )
A. ![]() 有最大值和最小值
有最大值和最小值
B. ![]() 的圖象的對稱中心為
的圖象的對稱中心為![]() (
(![]() )
)
C. ![]() 在
在![]() 上存在單調(diào)遞減區(qū)間
上存在單調(diào)遞減區(qū)間
D. ![]() 的圖象可由
的圖象可由![]() 的圖象向左平移
的圖象向左平移![]() 個(gè)單位而得
個(gè)單位而得
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知鮮切花![]() 的質(zhì)量等級按照花枝長度
的質(zhì)量等級按照花枝長度![]() 進(jìn)行劃分,劃分標(biāo)準(zhǔn)如下表所示.
進(jìn)行劃分,劃分標(biāo)準(zhǔn)如下表所示.
花枝長度 |
|
|
|
鮮花等級 | 三級 | 二級 | 一級 |
某鮮切花加工企業(yè)分別從甲乙兩個(gè)種植基地購進(jìn)鮮切花![]() ,現(xiàn)從兩個(gè)種植基地購進(jìn)的鮮切花
,現(xiàn)從兩個(gè)種植基地購進(jìn)的鮮切花![]() 中分別隨機(jī)抽取30個(gè)樣品,測量花枝長度并進(jìn)行等級評定,所抽取樣品數(shù)據(jù)如圖所示.
中分別隨機(jī)抽取30個(gè)樣品,測量花枝長度并進(jìn)行等級評定,所抽取樣品數(shù)據(jù)如圖所示.
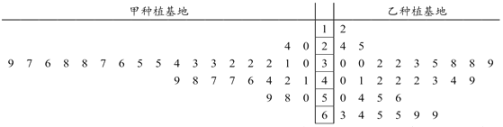
(1)根據(jù)莖葉圖比較兩個(gè)種植基地鮮切花![]() 的花枝長度的平均值及分散程度(不要求計(jì)算具體值,給出結(jié)論即可);
的花枝長度的平均值及分散程度(不要求計(jì)算具體值,給出結(jié)論即可);
(2)若從等級為三級的樣品中隨機(jī)選取2個(gè)進(jìn)行新產(chǎn)品試加工,求選取的2個(gè)全部來自乙種植基地的概率;
(3)根據(jù)該加工企業(yè)的加工和銷售記錄,了解到來自乙種植基地的鮮切花![]() 的加工產(chǎn)品的單件利潤為4元;來自乙種植基地的鮮切花
的加工產(chǎn)品的單件利潤為4元;來自乙種植基地的鮮切花![]() 的加工產(chǎn)品的單件成本為10元,銷售率(某等級產(chǎn)品的銷量與產(chǎn)量的比值)及單價(jià)如下表所示.
的加工產(chǎn)品的單件成本為10元,銷售率(某等級產(chǎn)品的銷量與產(chǎn)量的比值)及單價(jià)如下表所示.
三級花加工產(chǎn)品 | 二級花加工產(chǎn)品 | 一級花加工產(chǎn)品 | |
銷售率 |
|
|
|
單價(jià)/(元/件) | 12 | 16 | 20 |
由于鮮切花![]() 加工產(chǎn)品的保鮮特點(diǎn),未售出的產(chǎn)品均可按原售價(jià)的50%處理完畢.用樣本估計(jì)總體,如果僅從單件產(chǎn)品的利潤的角度考慮,該鮮切花加工企業(yè)應(yīng)該從哪個(gè)種植基地購進(jìn)鮮切花
加工產(chǎn)品的保鮮特點(diǎn),未售出的產(chǎn)品均可按原售價(jià)的50%處理完畢.用樣本估計(jì)總體,如果僅從單件產(chǎn)品的利潤的角度考慮,該鮮切花加工企業(yè)應(yīng)該從哪個(gè)種植基地購進(jìn)鮮切花![]() ?
?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com