
【題目】已知函數![]() ,
,![]() .
.
(1)若![]() 在
在![]() 上為單調遞增,求實數
上為單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() ,且
,且![]() ,求證:對定義域內的任意實數
,求證:對定義域內的任意實數![]() ,不等式
,不等式![]() 恒成立.
恒成立.
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)根據函數單調遞增可得![]() ,將問題轉化為
,將問題轉化為![]() 在
在![]() 上恒成立;利用導數求解出
上恒成立;利用導數求解出![]() 在
在![]() 的最小值,從而得到
的最小值,從而得到![]() 的取值范圍;(2)將問題轉化為證明當
的取值范圍;(2)將問題轉化為證明當![]() 時,
時,![]() ,在
,在![]() 和
和![]() 時分別得到需恒成立的不等式;令
時分別得到需恒成立的不等式;令![]() ,通過導數研究
,通過導數研究![]() 單調性,結合
單調性,結合![]() 可證得結論.
可證得結論.
(1)由已知![]() 的定義域為
的定義域為![]()
所以![]()
![]() 在
在![]() 上單調遞增
上單調遞增
![]() 對任意
對任意![]() ,都有
,都有![]()
![]()
即![]()
令![]() ,
,![]()
![]() 當
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
![]() 函數
函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減
上單調遞減
因為![]() 時,總有
時,總有![]()
![]()
![]()
(2)當![]() 時,
時,![]()
對定義域內的任意正數![]() ,不等式
,不等式![]() 恒成立,即
恒成立,即![]() 時,
時,![]()
因為當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以只須證:當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
令![]()
![]()
令![]() ,則
,則![]()
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
所以![]() 是
是![]() 的極值點,從而
的極值點,從而![]() 有極小值,即最小值
有極小值,即最小值![]()
所以![]() 恒成立
恒成立
![]() 在
在![]() 上單調遞增,又因為
上單調遞增,又因為![]()
所以當![]() 時,
時,![]() ,即
,即![]() 恒成立;
恒成立;
當![]() 時,
時,![]() ,即
,即![]() 恒成立
恒成立
所以,對定義域內的任意實數![]() ,不等式
,不等式![]() 恒成立
恒成立


科目:高中數學 來源: 題型:
【題目】今年3月5日,國務院總理李克強作的政府工作報告中,提到要“懲戒學術不端,力戒學術不端,力戒浮躁之風”.教育部日前公布的《教育部2019年部門預算》中透露,2019年教育部擬抽檢博士學位論文約6000篇,預算為800萬元.國務院學位委員會、教育部2014年印發的《博士碩士學位論文抽檢辦法》通知中規定:每篇抽檢的學位論文送3位同行專家進行評議,3位專家中有2位以上(含2位)專家評議意見為“不合格”的學位論文,將認定為“存在問題學位論文”.有且只有1位專家評議意見為“不合格”的學位論文,將再送2位同行專家進得復評,2位復評專家中有1位以上(含1位)專家評議意見為“不合格”的學位論文,將認定為“存在問題學位論文”.設每篇學位論文被每位專家評議為“不合格”的概率均為![]() ,且各篇學位論文是否被評議為“不合格”相互獨立.
,且各篇學位論文是否被評議為“不合格”相互獨立.
(1)記一篇抽檢的學位論文被認定為“存在問題學位論文”的概率為![]() ,求
,求![]() ;
;
(2)若擬定每篇抽檢論文不需要復評的評審費用為900元,需要復評的評審費用為1500元;除評審費外,其它費用總計為100萬元.現以此方案實施,且抽檢論文為6000篇,問是否會超過預算?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某技術人員在某基地培育了一種植物,一年后,該技術人員從中隨機抽取了部分這種植物的高度(單位:厘米)作為樣本(樣本容量為![]() )進行統計,繪制了如下頻率分布直方圖,已知抽取的樣本植物高度在
)進行統計,繪制了如下頻率分布直方圖,已知抽取的樣本植物高度在![]() 內的植物有8株,在
內的植物有8株,在![]() 內的植物有2株.
內的植物有2株.

(Ⅰ)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() ,
,![]() 的值;
的值;
(Ⅱ)在選取的樣本中,從高度在![]() 內的植物中隨機抽取3株,設隨機變量
內的植物中隨機抽取3株,設隨機變量![]() 表示所抽取的3株高度在
表示所抽取的3株高度在![]() 內的株數,求隨機變量
內的株數,求隨機變量![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅲ)據市場調研,高度在![]() 內的該植物最受市場追捧.老王準備前往該基地隨機購買該植物50株.現有兩種購買方案,方案一:按照該植物的不同高度來付費,其中高度在
內的該植物最受市場追捧.老王準備前往該基地隨機購買該植物50株.現有兩種購買方案,方案一:按照該植物的不同高度來付費,其中高度在![]() 內的每株10元,其余高度每株5元;方案二:按照該植物的株數來付費,每株6元.請你根據該基地該植物樣本的統計分析結果為決策依據,預測老王采取哪種付費方式更便宜?
內的每株10元,其余高度每株5元;方案二:按照該植物的株數來付費,每株6元.請你根據該基地該植物樣本的統計分析結果為決策依據,預測老王采取哪種付費方式更便宜?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,當
上的奇函數,當![]() 時,
時,![]() .則下列結論正確的是( ).
.則下列結論正確的是( ).
A.當![]() 時,
時,![]()
B.函數![]() 有五個零點
有五個零點
C.若關于![]() 的方程
的方程![]() 有解,則實數
有解,則實數![]() 的取值范圍是
的取值范圍是![]()
D.對![]() ,
,![]() 恒成立
恒成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,四邊形
,四邊形![]() 滿足
滿足![]() 且
且![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 為
為![]() 邊上的動點,且
邊上的動點,且![]() .
.
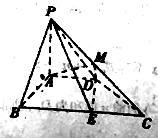
(1)求證:平面![]() 平面
平面![]() ;
;
(2)是否存在實數![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,試求出實數
?若存在,試求出實數![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知p:x2-(3+a)x+3a<0,其中a<3;q:x2+4x-5>0.
(1)若p是q的必要不充分條件,求實數a的取值范圍;
(2)若p是q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com