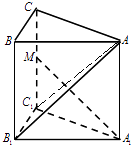
【題目】直三棱柱ABC﹣A1B1C1中，∠ACB=90°，∠BAC=30°，BC=1，AA1= 
，M是CC1的中點，則異面直線AB1與A1M所成角為 ．
【答案】
【解析】解：連接AC1
∵∠ACB=90°，∠BAC=30°，BC=1，AA1= 
，
∴A1C1= 
BC= ，
Rt△A1C1M中，tan∠A1MC1= 
；
Rt△AA1C1中，tan∠AC1A1=
∴tan∠MA1C1=tan∠AC1A1 即∠AC1A1=∠A1MC1
可得矩形AA1C1C中，A1M⊥AC1
∵B1C1⊥A1C1 ， B1C1⊥CC1且AC1∩CC1=C1
∴B1C1⊥平面AA1C1 ，
∵A1M面AA1C1 ， ∴B1C1⊥A1M，
又AC1∩B1C1=C1 ， ∴A1M⊥平面AB1C1
結合AB1平面AB1C1 ， 得到AB1⊥A1M，
即異面直線AB1與A1M所成的角是 ．
所以答案是： ．
【考點精析】關于本題考查的異面直線及其所成的角，需要了解異面直線所成角的求法：1、平移法：在異面直線中的一條直線中選擇一特殊點，作另一條的平行線；2、補形法：把空間圖形補成熟悉的或完整的幾何體，如正方體、平行六面體、長方體等，其目的在于容易發現兩條異面直線間的關系才能得出正確答案．
口算題卡北京婦女兒童出版社系列答案科目：高中數學 來源： 題型：
【題目】據市場調查，某種商品一年內每件出廠價在7千元的基礎上，按月呈f（x）＝Asin（ωx＋
）＋b （A＞0，ω＞0，｜ 
｜＜
）的模型波動（x為月份），已知3月份達到最高價9千元，7月份價格最低為5千元，根據以上條件可確定f（x）的解析式為
A. f（x）＝2sin（
x－
）＋7 （1≤x≤12，x∈N＋）
B. f（x）＝9sin（
x－
） （1≤x≤12，x∈N＋）
C. f（x）＝2
sin
x＋7 （1≤x≤12，x∈N＋）
D. f（x）＝2sin（
x＋
）＋7 （1≤x≤2，x∈N＋）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某大學藝術專業400名學生參加某次測評，根據男女學生人數比例，使用分層抽樣的方法從中隨機抽取了100名學生，記錄他們的分數，將數據分成7組：[20,30），[30,40），┄，[80,90]，并整理得到如下頻率分布直方圖：
（Ⅰ）從總體的400名學生中隨機抽取一人，估計其分數小于70的概率；
（Ⅱ）已知樣本中分數小于40的學生有5人，試估計總體中分數在區間[40,50）內的人數；
（Ⅲ）已知樣本中有一半男生的分數不小于70，且樣本中分數不小于70的男女生人數相等．試估計總體中男生和女生人數的比例．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2+4[sin（θ+ 
）]x﹣2，θ∈[0，2π]]．
（1）若函數f（x）為偶函數，求tanθ的值；
（2）若f（x）在[﹣ 
，1]上是單調函數，求θ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設關于x的一元二次方程x2+2ax+b2=0．
（1）若a是從0，1，2，3四個數中任取的一個數，b是從0，1，2三個數中任取的一個數，求上述方程有實根的概率．
（2）若a是從區間[0，3]任取的一個數，b是從區間[0，2]任取的一個數，求上述方程有實根的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
