
【題目】2017年“一帶一路”國際合作高峰論壇于今年5月14日至15日在北京舉行.為高標準完成高峰論壇會議期間的志愿服務工作,將從27所北京高校招募大學生志愿者,某調查機構從是否有意愿做志愿者在某高校訪問了80人,經過統計,得到如下丟失數據的列聯表:(![]() ,表示丟失的數據)
,表示丟失的數據)
無意愿 | 有意愿 | 總計 | |
男 |
|
| 40 |
女 | 5 |
|
|
總計 | 25 |
| 80 |
(1)求出![]() 的值,并判斷:能否有99.9%的把握認為有意愿做志愿者與性別有關;
的值,并判斷:能否有99.9%的把握認為有意愿做志愿者與性別有關;
(2)若表中無意愿做志愿者的5個女同學中,3個是大學三年級同學,2個是大學四年級同學.現從這5個同學中隨機選2同學進行進一步調查,求這2個同學是同年級的概率.
附參考公式及數據: 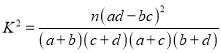 ,其中
,其中![]() .
.
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
科目:高中數學 來源: 題型:
【題目】國內某汽車品牌一個月內被消費者投訴的次數用![]() 表示,據統計,隨機變量
表示,據統計,隨機變量![]() 的概率分布如下:
的概率分布如下:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值;
的值;
(2)假設一月與二月被消費者投訴的次數互不影響,求該汽車品牌在這兩個月內被消費者投訴![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·全國卷Ⅲ文,18)某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:℃)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間[20,25),需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
最高氣溫 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區間的頻率估計最高氣溫位于該區間的概率.
(1)估計六月份這種酸奶一天的需求量不超過300瓶的概率;
(2)設六月份一天銷售這種酸奶的利潤為Y(單位:元).當六月份這種酸奶一天的進貨量為450瓶時,寫出Y的所有可能值,并估計Y大于零的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分組的頻率分布直方圖如圖所示.

(1)求直方圖中x的值;
(2)求月平均用電量的眾數和中位數;
(3)在月平均用電量為[220,240),[240,260),[260,280),[280,300]的四組用戶中,用分層抽樣的方法抽取11戶居民,則月平均用電量在[220,240)的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() 為參數).它與曲線
為參數).它與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求![]() 的長;
的長;
(2)在以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,設點
軸的正半軸為極軸建立極坐標系,設點![]() 的極坐標為
的極坐標為![]() ,求點
,求點![]() 到線段
到線段![]() 中點
中點![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為了更好地了解設備改造前后與生產合格品的關系,隨機抽取了180件產品進行分析,其中設備改造前的合格品有36件,不合格品有49件,設備改造后生產的合格品有65件,不合格品有30件.根據所給數據:
⑴寫出![]() 列聯表;⑵判斷產品是否合格與設備改造是否有關,說明理由.
列聯表;⑵判斷產品是否合格與設備改造是否有關,說明理由.
附: 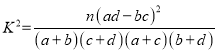 ,
,
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,直線
,直線![]() 是函數
是函數![]() 圖象的一條對稱軸.
圖象的一條對稱軸.
(1)求![]() 的值,并求
的值,并求![]() 的解析式;
的解析式;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有且只有一個實數解,求實數
上有且只有一個實數解,求實數![]() 的取值范圍;
的取值范圍;
(3)已知函數![]() 的圖象是由
的圖象是由![]() 圖象上的所有點的橫坐標伸長到原來的2倍,然后再向左平移
圖象上的所有點的橫坐標伸長到原來的2倍,然后再向左平移![]() 個單位得到,若
個單位得到,若![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com