
【題目】已知函數![]()
求證:(1)![]()
(2)對![]() ,若
,若![]() ,
,![]() =1,求證:
=1,求證: ![]()
【答案】(1)見解析;(2)見解析.
【解析】試題分析:
(1)利用函數的單調性結合函數的定義域即可證得結論;
(2)結合題意利用數學歸納法證明結論即可.
試題解析:
⑴x>0時,![]() =x
=x![]()
![]() 0,f(x)單調增,f(x)
0,f(x)單調增,f(x) ![]() f(0)=0
f(0)=0
⑵①![]()
![]()
![]() =
=![]() , x1=1
, x1=1![]()
![]() >1,
>1,![]() >0對任意n成立;
>0對任意n成立;
又⑴知f(![]() )
)![]() 0
0![]()
![]() -1<
-1<![]() ,從而
,從而![]() <
<![]() ,
,![]() ,數列{
,數列{![]() }單調減,
}單調減,
②下面用數學歸納法證明![]()
當n=1時,![]() =1>
=1>![]() ,命題成立
,命題成立
假設n=k時,命題成立,即![]()
要證![]() >
>![]() ,只要證明
,只要證明![]() ,只要證明
,只要證明![]() >
>![]()
設g(x)=![]() ,
,![]() =
=![]() =-
=-![]() >0在x>0上成立,
>0在x>0上成立,
故g(x)在x>0上單調增,![]() ,g(
,g(![]() )=
)=![]() >g(
>g(![]() ),
),
只要證明g(![]() )=
)=![]() >
>![]() =
=![]() ,設
,設![]() ≥
≥![]() =t>0,
=t>0,
只要證明![]() ,只要證明
,只要證明![]() -1>t
-1>t![]()
設![]() -1-t
-1-t![]() =h(t),t>0,
=h(t),t>0,![]() =
=![]() >0在t>0時恒成立,
>0在t>0時恒成立,
h(t)單調增,h(t)>h(0)=0, ![]() -1>t
-1>t![]() 成立。從而對n=k+1,不等式仍然成立
成立。從而對n=k+1,不等式仍然成立
總之,![]() 成立
成立


 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 在平面直角坐標系
在平面直角坐標系![]() 下的參數方程為
下的參數方程為 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的普通方程及極坐標方程;
的普通方程及極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
: ![]() 與曲線
與曲線![]() 交于點
交于點![]() 與直線
與直線![]() 交于點
交于點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,點M,N分別在PB,PC上,且MN∥BC. 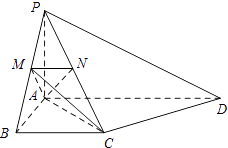
(1)證明:平面AMN⊥平面PBA;
(2)若M為PB的中點,求二面角M﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究所設計了一款智能機器人,為了檢驗設計方案中機器人動作完成情況,現委托某工廠生產![]() 個機器人模型,并對生產的機器人進行編號:
個機器人模型,并對生產的機器人進行編號: ![]() ,采用系統抽樣的方法抽取一個容量為
,采用系統抽樣的方法抽取一個容量為![]() 的機器人樣本,試驗小組對
的機器人樣本,試驗小組對![]() 個機器人樣本的動作個數進行分組,頻率分布直方圖及頻率分布表中的部分數據如圖所示,請據此回答如下問題:
個機器人樣本的動作個數進行分組,頻率分布直方圖及頻率分布表中的部分數據如圖所示,請據此回答如下問題:
分組 | 機器人數 | 頻率 |
| 0.08 | |
| 10 | |
| 10 | |
| ||
| 6 |

(1)補全頻率分布表,畫出頻率分布直方圖;
(2)若隨機抽的第一個號碼為![]() ,這
,這![]() 個機器人分別放在
個機器人分別放在![]() 三個房間,從
三個房間,從![]() 到
到![]() 在
在![]() 房間,從
房間,從![]() 到
到![]() 在
在![]() 房間,從
房間,從![]() 到
到![]() 在
在![]() 房間,求
房間,求![]() 房間被抽中的人數是多少?
房間被抽中的人數是多少?
(3)從動作個數不低于![]() 的機器人中隨機選取
的機器人中隨機選取![]() 個機器人,該
個機器人,該![]() 個機器人中動作個數不低于
個機器人中動作個數不低于![]() 的機器人記為
的機器人記為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列不等關系正確的是( )
A.( ![]() )
) ![]() <34<(
<34<( ![]() )﹣2
)﹣2
B.( ![]() )﹣2<(
)﹣2<( ![]() )
) ![]() <34
<34
C.(2.5)0<( ![]() )2.5<22.5
)2.5<22.5
D.( ![]() )2.5<(2.5)0<22.5
)2.5<(2.5)0<22.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 中,
中, ![]() 是橢圓的左、右焦點,過
是橢圓的左、右焦點,過![]() 作直線
作直線![]() 交橢圓于
交橢圓于![]() 兩點,若
兩點,若![]() 的周長為8,離心率為
的周長為8,離心率為![]() .
.
(1)求橢圓方程;
(2)若弦![]() 的斜率不為0,且它的中垂線與
的斜率不為0,且它的中垂線與![]() 軸交于
軸交于![]() ,求
,求![]() 的縱坐標的范圍;
的縱坐標的范圍;
(3)是否在![]() 軸上存在點
軸上存在點![]() ,使得
,使得![]() 軸平分
軸平分![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() ,且f(﹣2)=3,f(﹣1)=f(1).
,且f(﹣2)=3,f(﹣1)=f(1).
( I)求f(x)的解析式;
( II)畫出f(x)的圖象(不寫過程)并求其值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行抽獎活動,規則如下:甲箱子里裝有3個白球和2個黑球,乙箱子里裝有1個白球和3個黑球,這些球除顏色外完全相同;每次抽獎都從這兩個箱子里各隨機地摸出2個球,若摸出的白球個數不少于2個,則獲獎.(每次游戲結束后將球放回原箱)
(1)在一次游戲中,求獲獎的概率;
(2)在三次游戲中,記獲獎次數為隨機變量X,求X的分布列及期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com