
【題目】如圖1,已知四邊形BCDE為直角梯形,![]() ,
,![]() ,且
,且![]() ,A為BE的中點
,A為BE的中點![]() 將
將![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如圖
如圖![]() ,連結PC,PB構成一個四棱錐
,連結PC,PB構成一個四棱錐![]() .
.

![]() Ⅰ
Ⅰ![]() 求證
求證![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在點M,滿足
在棱PC上存在點M,滿足![]() ,使得直線AM與平面PBC所成的角為
,使得直線AM與平面PBC所成的角為![]() ,求
,求![]() 的值.
的值.
【答案】![]() Ⅰ
Ⅰ![]() 詳見解析;
詳見解析;![]() Ⅱ
Ⅱ![]() ①
①![]() ,②
,②![]() 或
或![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 可以通過已知證明出
可以通過已知證明出![]() 平面PAB,這樣就可以證明出
平面PAB,這樣就可以證明出![]() ;
;
![]() Ⅱ
Ⅱ![]() 以點A為坐標原點,分別以AB,AD,AP為x,y,z軸,建立空間直角坐標系,可以求出相應點的坐標,求出平面PBC的法向量為
以點A為坐標原點,分別以AB,AD,AP為x,y,z軸,建立空間直角坐標系,可以求出相應點的坐標,求出平面PBC的法向量為![]() 、平面PCD的法向量
、平面PCD的法向量![]() ,利用空間向量的數量積,求出二面角
,利用空間向量的數量積,求出二面角![]() 的大小;
的大小;
![]() 求出平面PBC的法向量,利用線面角的公式求出
求出平面PBC的法向量,利用線面角的公式求出![]() 的值.
的值.
證明:![]() Ⅰ
Ⅰ![]() 在圖1中,
在圖1中,![]() ,
,![]() ,
,

![]() 為平行四邊形,
為平行四邊形,![]() ,
,
![]() ,
,![]() ,
,
當![]() 沿AD折起時,
沿AD折起時,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() 平面PAB,
平面PAB,
又![]() 平面PAB,
平面PAB,![]() .
.
解:![]() Ⅱ
Ⅱ![]() 以點A為坐標原點,分別以AB,AD,AP為x,y,z軸,建立空間直角坐標系,由于
以點A為坐標原點,分別以AB,AD,AP為x,y,z軸,建立空間直角坐標系,由于![]() 平面ABCD
平面ABCD
則![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]()
![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
設平面PBC的法向量為![]() y,
y,![]() ,
,
則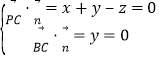 ,取
,取![]() ,得
,得![]() 0,
0,![]() ,
,
設平面PCD的法向量![]() b,
b,![]() ,
,
則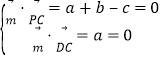 ,取
,取![]() ,得
,得![]() 1,
1,![]() ,
,
設二面角![]() 的大小為
的大小為![]() ,可知為鈍角,
,可知為鈍角,
則![]() ,
,![]() .
.
![]() 二面角
二面角![]() 的大小為
的大小為![]() .
.
![]() 設AM與面PBC所成角為
設AM與面PBC所成角為![]() ,
,
![]() 0,
0,![]() ,1,
,1,![]() ,
,![]() ,
,![]() ,
,
平面PBC的法向量![]() 0,
0,![]() ,
,
![]() 直線AM與平面PBC所成的角為
直線AM與平面PBC所成的角為![]() ,
,
![]() ,
,
解得![]() 或
或![]() .
.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四面體A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2 ![]() .M是AD的中點,P是BM的中點,點Q在線段AC上,且AQ=3QC.
.M是AD的中點,P是BM的中點,點Q在線段AC上,且AQ=3QC. 
(1)證明:PQ∥平面BCD;
(2)若二面角C﹣BM﹣D的大小為60°,求∠BDC的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學舉行了一次“環保知識競賽”活動.為了了解本次競賽學生成績情況,從中抽取了部分學生的分數(得分取正整數,滿分為100分)作為樣本(樣本容量為n)進行統計.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出了得分在[50,60),[90,100]的數據).
(1)求樣本容量n和頻率分布直方圖中x、y的值;
(2)根據樣本直方圖估計所取樣本的中位數及平均數(同一組數據用該區間的中點值作代表).

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】位于濰坊濱海的“濱海之眼”摩天輪是世界上最高的無軸摩天輪,該摩天輪的直徑均為124米,中間沒有任何支撐,摩天輪順時針勻速旋轉一圈需要30分鐘,當乘客乘坐摩天輪到達最高點時,距離地面145米,可以俯瞰白浪河全景,圖中![]() 與地面垂直,垂足為點
與地面垂直,垂足為點![]() ,某乘客從
,某乘客從![]() 處進入
處進入![]() 處的觀景艙,順時針轉動
處的觀景艙,順時針轉動![]() 分鐘后,第1次到達
分鐘后,第1次到達![]() 點,此時
點,此時![]() 點與地面的距離為114米,則
點與地面的距離為114米,則![]() ( )
( )

A. 16分鐘B. 18分鐘C. 20分鐘D. 22分鐘
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,“共享單車”的出現為市民“綠色出行”提供了極大的方便,某共享單車公司“Mobike”計劃在甲、乙兩座城市共投資120萬元,根據行業規定,每個城市至少要投資40萬元,由前期市場調研可知:甲城市收益P與投入a(單位:萬元)滿足![]() ,乙城市收益Q與投入a(單位:萬元)滿足
,乙城市收益Q與投入a(單位:萬元)滿足![]() ,設甲城市的投入為x(單位:萬元),兩個城市的總收益為
,設甲城市的投入為x(單位:萬元),兩個城市的總收益為![]() (單位:萬元).
(單位:萬元).
(1)求![]() 及定義域;
及定義域;
(2)試問如何安排甲、乙兩個城市的投資,才能使總收益最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a為實常數,y=f(x)是定義在R上的奇函數,當x<0時,f(x)=9x+ ![]() +7.若f(x)≥a+1對一切x≥0成立,則a的取值范圍為 .
+7.若f(x)≥a+1對一切x≥0成立,則a的取值范圍為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著手機的普及,大學生迷戀手機的現象非常嚴重.為了調查雙休日大學生使用手機的時間,某機構采用不記名方式隨機調查了使用手機時間不超過![]() 小時的
小時的![]() 名大學生,將
名大學生,將![]() 人使用手機的時間分成
人使用手機的時間分成![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別加以統計,得到下表,根據數據完成下列問題:
分別加以統計,得到下表,根據數據完成下列問題:
使用時間/時 |
|
|
|
|
|
大學生/人 |
|
|
|
|
|

(1)完成頻率分布直方圖;
(2)根據頻率分布直方圖估計大學生使用手機的平均時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線C1: ![]() 的焦點與雙曲線C2:
的焦點與雙曲線C2: ![]() 的右焦點的連線交C1于第一象限的點M.若C1在點M處的切線平行于C2的一條漸近線,則p=( )
的右焦點的連線交C1于第一象限的點M.若C1在點M處的切線平行于C2的一條漸近線,則p=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com