
【題目】過點(diǎn)![]() 的直線
的直線![]() 與
與![]() 軸正半軸和
軸正半軸和![]() 軸正半軸分別交于
軸正半軸分別交于![]() ,
,![]()
(1)當(dāng)![]() 為
為![]() 的中點(diǎn)時(shí),求
的中點(diǎn)時(shí),求![]() 的方程
的方程
(2)當(dāng)![]() 最小時(shí),求
最小時(shí),求![]() 的方程
的方程
(3)當(dāng)![]() 面積取到最小值時(shí),求
面積取到最小值時(shí),求![]() 的方程
的方程
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)設(shè)![]() ,
,![]() ,由
,由![]() 為
為![]() 的中點(diǎn),求出
的中點(diǎn),求出![]() ,再寫方程. (2)設(shè)所求直線的方程為
,再寫方程. (2)設(shè)所求直線的方程為![]() ,求出
,求出![]() ,
,![]() ,表示出
,表示出![]() ,用均值定理即可
,用均值定理即可
(3)設(shè)直線的截距式方程為![]() ,由
,由![]() 用均值定理即可.
用均值定理即可.
解:(1)設(shè)![]() ,
,![]() ,
,
∵![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),
∴![]() ,
,![]() ,
,
∴由截距式得![]() 的方程為:
的方程為:![]() ,
,
即![]() ;
;
(2)設(shè)所求直線的方程為![]() ,由題意知
,由題意知![]() ,
,
令![]() 可得
可得![]() ,令
,令![]() 可得
可得![]() ,
,
即![]() ,
,![]() .
.
∴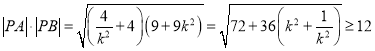 ,
,
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時(shí)取等號,
時(shí)取等號,![]() 取最小值為12,
取最小值為12,
即直線![]() 的方程為
的方程為![]() ;
;
(3)由題意設(shè)直線的截距式方程為![]() ,
,
∵直線過![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
當(dāng)且僅當(dāng)![]() 即
即![]() 且
且![]() 時(shí)取等號,
時(shí)取等號,
∴![]() 的面積
的面積![]() ,
,
∴![]() 面積的最小值為12,此時(shí)直線
面積的最小值為12,此時(shí)直線![]() 的方程為
的方程為![]() ,
,
即直線![]() 的方程為
的方程為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)點(diǎn)P是函數(shù)![]() 圖象上任意一點(diǎn),點(diǎn)Q坐標(biāo)為
圖象上任意一點(diǎn),點(diǎn)Q坐標(biāo)為![]() ,當(dāng)
,當(dāng)![]() 取得最小值時(shí)圓
取得最小值時(shí)圓![]() 與圓
與圓![]() 相外切,則
相外切,則![]() 的最大值為
的最大值為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“砥礪奮進(jìn)的五年”,首都經(jīng)濟(jì)社會(huì)發(fā)展取得新成就.自2012年以來,北京城鄉(xiāng)居民收入穩(wěn)步增長.隨著擴(kuò)大內(nèi)需,促進(jìn)消費(fèi)等政策的出臺(tái),居民消費(fèi)支出全面增長,消費(fèi)結(jié)構(gòu)持續(xù)優(yōu)化升級,城鄉(xiāng)居民人均可支配收入快速增長,人民生活品質(zhì)不斷提升.下圖是北京市2012-2016年城鄉(xiāng)居民人均可支配收入實(shí)際增速趨勢圖(例如2012年,北京城鎮(zhèn)居民收入實(shí)際增速為7.3%,農(nóng)村居民收入實(shí)際增速為8.2%).
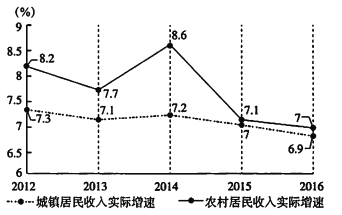
(Ⅰ)從2012-2016五年中任選一年,求城鎮(zhèn)居民收入實(shí)際增速大于7%的概率;
(Ⅱ)從2012-2016五年中任選一年,求至少有一年農(nóng)村和城鎮(zhèn)居民收入實(shí)際增速均超過7%的概率;
(Ⅲ)由圖判斷,從哪年開始連續(xù)三年農(nóng)村居民收入實(shí)際增速方差最大?(結(jié)論不要求證明)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(Ⅱ)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)若對于任意![]() ,都有
,都有![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在幾何體![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為菱形,且
為菱形,且![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 中點(diǎn).
中點(diǎn).
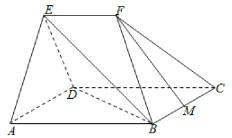
(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的離心率為
)的離心率為![]() ,短軸端點(diǎn)到焦點(diǎn)的距離為
,短軸端點(diǎn)到焦點(diǎn)的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() ,
,![]() 為橢圓
為橢圓![]() 上任意兩點(diǎn),
上任意兩點(diǎn),![]() 為坐標(biāo)原點(diǎn),且
為坐標(biāo)原點(diǎn),且![]() .求證:原點(diǎn)
.求證:原點(diǎn)![]() 到直線
到直線![]() 的距離為定值,并求出該定值.
的距離為定值,并求出該定值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com