
【題目】基于移動(dòng)網(wǎng)絡(luò)技術(shù)的共享單車被稱為“新四大發(fā)明”之一,短時(shí)間內(nèi)就風(fēng)靡全國,給人們帶來新的出行體驗(yàn),某共享單車運(yùn)營公司的市場研究人員為了了解公司的經(jīng)營狀況,對(duì)公司最近6個(gè)月的市場占有率![]() 進(jìn)行了統(tǒng)計(jì),結(jié)果如下表:
進(jìn)行了統(tǒng)計(jì),結(jié)果如下表:
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
(1)請(qǐng)用相關(guān)系數(shù)說明能否用線性回歸模型擬合![]() 與月份代碼
與月份代碼![]() 之間的關(guān)系.如果能,請(qǐng)計(jì)算出
之間的關(guān)系.如果能,請(qǐng)計(jì)算出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程,如果不能,請(qǐng)說明理由;
的線性回歸方程,如果不能,請(qǐng)說明理由;
(2)根據(jù)調(diào)研數(shù)據(jù),公司決定再采購一批單車擴(kuò)大市場,從成本1000元/輛的![]() 型車和800元/輛的
型車和800元/輛的![]() 型車中選購一種,兩款單車使用壽命頻數(shù)如下表:
型車中選購一種,兩款單車使用壽命頻數(shù)如下表:
| 1年 | 2年 | 3年 | 4年 | 總計(jì) |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
經(jīng)測算,平均每輛單車每年能為公司帶來500元的收入,不考慮除采購成本以外的其它成本,假設(shè)每輛單車的使用壽命都是整數(shù)年,用頻率估計(jì)每輛車使用壽命的概率,以平均每輛單車所產(chǎn)生的利潤的估計(jì)值為決策依據(jù),如果你是公司負(fù)責(zé)人,會(huì)選擇哪款車型?
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關(guān)系數(shù)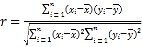 ,
,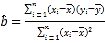 ,
,![]() .
.
【答案】(1)見解析;(2)采購![]() 款車型.
款車型.
【解析】
(1)求出相關(guān)系數(shù),判斷即可,求出回歸方程的系數(shù),即可得到![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)分別求出A,B的平均利潤,判斷即可.
解:(1)由表格中數(shù)據(jù)可得,![]() ,
,![]() .
.
∵
![]() .
.
∴![]() 與月份代碼
與月份代碼![]() 之間具有較強(qiáng)的相關(guān)關(guān)系,故可用線性回歸模型擬合兩變量之間的關(guān)系.
之間具有較強(qiáng)的相關(guān)關(guān)系,故可用線性回歸模型擬合兩變量之間的關(guān)系.
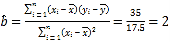 ,
,
∴![]() ,
,
∴關(guān)于![]() 的線性回歸方程為
的線性回歸方程為![]() .
.
(2)這100輛![]() 款單車平均每輛的利潤為
款單車平均每輛的利潤為
![]() (元)
(元)
這100輛![]() 款單車平均每輛的利潤為
款單車平均每輛的利潤為
![]() (元)
(元)
∴用頻率估計(jì)概率,![]() 款單車與
款單車與![]() 款單車平均每輛的利潤估計(jì)值分別為350元、400元,應(yīng)采購
款單車平均每輛的利潤估計(jì)值分別為350元、400元,應(yīng)采購![]() 款車型.
款車型.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]()
(1)已知![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,在區(qū)間
上單調(diào)遞減,在區(qū)間![]() 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
(2)若對(duì)任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國古代儒家提出的“六藝”指:禮樂射御書數(shù).某校國學(xué)社團(tuán)預(yù)在周六開展“六藝”課程講座活動(dòng),周六這天準(zhǔn)備排課六節(jié),每藝一節(jié),排課有如下要求:“樂”與“書”不能相鄰,“射”和“御”要相鄰,則針對(duì)“六藝”課程講座活動(dòng)的不同排課順序共有( )
A.18種B.36種C.72種D.144種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)求函數(shù)![]() 的極值;
的極值;
(2)若![]() 在
在![]() 上為單調(diào)函數(shù),求
上為單調(diào)函數(shù),求![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() ,若在
,若在![]() 上至少存在一個(gè)
上至少存在一個(gè)![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 在
在![]() 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時(shí),若方程
時(shí),若方程![]() 有兩個(gè)不等實(shí)數(shù)根
有兩個(gè)不等實(shí)數(shù)根![]() ,
,![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍,并證明
的取值范圍,并證明![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在三棱錐![]() 中,
中,![]() 與
與![]() 都是邊長為2的等邊三角形,
都是邊長為2的等邊三角形,![]() 是側(cè)棱
是側(cè)棱![]() 的中點(diǎn),過點(diǎn)
的中點(diǎn),過點(diǎn)![]() 作平行于
作平行于![]() 、
、![]() 的平面分別交棱
的平面分別交棱![]() 、
、![]() 、
、![]() 于點(diǎn)
于點(diǎn)![]() 、
、![]() 、
、![]() .
.
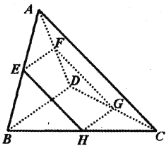
(1)證明:四邊形![]() 為矩形;
為矩形;
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱柱![]() 的底面為菱形,
的底面為菱形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點(diǎn).
的中點(diǎn).
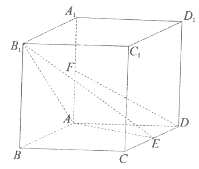
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,求異面直線
,求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com